题目内容
7.下列选项中,能使关于x的一元二次方程ax2-2x+c=0一定有实数根的是( )| A. | a>0 | B. | a=0 | C. | c=0 | D. | c>0 |
分析 由一元二次方程有实数根利用一元二次方程的定义结合根的判别式即可得出ac≤1且a≠0,再对每个选项逐一判断即可.
解答 解:∵关于x的一元二次方程ax2-2x+c=0有实数根,
∴$\left\{\begin{array}{l}{a≠0}\\{△=(-2)^{2}-4ac=4-4ac≥0}\end{array}\right.$,
解得:ac≤1且a≠0.
A、若a>0,当a=1、c=5时,ac=5>1,此选项不符合题意;
B、a=0不符合一元二次方程的定义,此选项不符合题意;
C、若c=0,ac=0<1,此选项符合题意;
D、若c>0,当a=2、c=2时,ac=4>1,此选项不符合题意;
故选C.
点评 本题考查根的判别式依据一元二次方程的定义,掌握一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根是解答本题的关键.

练习册系列答案
相关题目
19.对于任意实数x,点P(x,x2+4x+3)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.能构成三角形的是( )
| A. | 2、3、4 | B. | 5、3、8 | C. | 1、3、5 | D. | 1、2、3 |
17.如果$\frac{a}{b}$=2,则$\frac{{a}^{2}-ab+{b}^{2}}{{a}^{2}+{b}^{2}}$的值等于( )
| A. | $\frac{4}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | 2 |
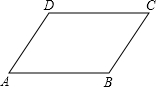 如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.
如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.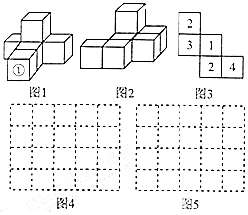 按要求完成下列问题:
按要求完成下列问题: