题目内容
12.已知一次函数y=-x+2与x轴、y轴分别交于点C、D,与反比例函数$y=\frac{k}{x}$交于A、B两点,其中OA=1.6,则k=0.72.分析 设点A的坐标为(m,n),根据一次函数以及反比例函数图象上点的坐标特征即可得出m+n=2、mn=1.6,再由两点间的距离公式即可得出关于k的一元一次方程,解之即可得出结论.
解答 解:设点A的坐标为(m,n).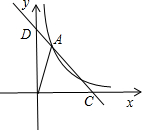
∵点A为一次函数y=-x+2与反比例函数$y=\frac{k}{x}$的交点,
∴n=-m+2,n=$\frac{k}{m}$,
∴m+n=2,mn=k.
∵OA=$\sqrt{{m}^{2}+{n}^{2}}$=1.6,
∴m2+n2=(m+n)2-2mn=4-2k=1.62=2.56,
解得:k=0.72.
故答案为:0.72.
点评 本题考查了反比例函数与一次函数的交点问题、反比例(一次)函数图象上点的坐标特征以及两点间的距离公式,利用两点间的距离公式结合OA=1.6找出关于k的一元一次方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
给出下列结论:
①m=-1
②当x>1时,y的值随x值的增大而减小
③3是方程ax2+(b-1)x+c=0的一个根
④若ax2+(b-1)x+c<0,则-1<x<3,其中正确的是( )
| X | -1 | 0 | 1 | 3 | 4 |
| y | -1 | 3 | 5 | 3 | m |
①m=-1
②当x>1时,y的值随x值的增大而减小
③3是方程ax2+(b-1)x+c=0的一个根
④若ax2+(b-1)x+c<0,则-1<x<3,其中正确的是( )
| A. | ①③ | B. | ③④ | C. | ①③④ | D. | ①②④ |
7.下列选项中,能使关于x的一元二次方程ax2-2x+c=0一定有实数根的是( )
| A. | a>0 | B. | a=0 | C. | c=0 | D. | c>0 |
1.下列计算正确的是( )
| A. | m(m-2)=m2-2 | B. | (a+1)2=a2+1 | ||
| C. | ${({-\frac{1}{2}a{b^2}})^3}=-\frac{1}{6}{a^3}{b^6}$ | D. | $\frac{m}{m-3}-\frac{m}{m-2}=\frac{m}{{{m^2}-5m+6}}$ |
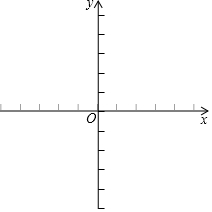 已知平行四边形的三个顶点的坐标分别为(1,1)(5,1)(2,4).请你在下面的坐标系中画出这三个点,根据这三个点的位置画出一个平行四边形,并写出第四个点的坐标.
已知平行四边形的三个顶点的坐标分别为(1,1)(5,1)(2,4).请你在下面的坐标系中画出这三个点,根据这三个点的位置画出一个平行四边形,并写出第四个点的坐标.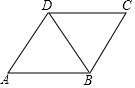 如图,在四边形ABCD中,∠A=∠C,AB=AD、BC=CD,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,AB=AD、BC=CD,求证:四边形ABCD是平行四边形.