题目内容
18.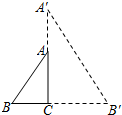 如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.
分析 △ACB沿直线AC翻折得到△ACD,如图,AA′=AB=5,在Rt△ACB中利用余弦定义计算出BC=3,利用勾股定理计算出AC=4,再利用翻折的性质得CD=CB=3,接着根据放大性质得到△ACD∽△A′CB′,利用相似比可求出CB′.
解答  解:△ACB沿直线AC翻折得到△ACD,如图,
解:△ACB沿直线AC翻折得到△ACD,如图,
∵△AA′B是等腰三角形,
∴AA′=AB=5,
在Rt△ACB中,∵cosB=$\frac{BC}{AB}$=$\frac{3}{5}$,
∵AB=5,
∴BC=3,
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵△ACB沿直线AC翻折得到△ACD,
∴CD=CB=3,
∵△ACD放大得到△A′CB′,
∴△ACD∽△A′CB′,
∴$\frac{AC}{CA′}$=$\frac{CD}{CB′}$,即$\frac{4}{4+5}$=$\frac{3}{B′C}$,
∴CB′=$\frac{27}{4}$.
故答案为$\frac{27}{4}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
3.设$6-\sqrt{13}$的整数部分为a,小数部分为b,那么2a-b的值是( )
| A. | $3-\sqrt{3}$ | B. | $4-\sqrt{13}$ | C. | $\sqrt{13}$ | D. | $4+\sqrt{13}$ |
10.我们规定,对于任意实数m,符号[m]表示小于或等于m的最大整数,例如:[2,1]=2,[2]=2,[-2,1]=-3,若对于整数x有[$\frac{3x-1}{2}$]=-5,则符合题意的x有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
7.7的平方根等于( )
| A. | $\sqrt{7}$ | B. | 49 | C. | ±49 | D. | ±$\sqrt{7}$ |
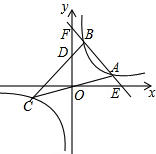 已知:一次函数y=-2x+10的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象相交于A,B两点(A在B的右侧).直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.$\frac{BC}{BD}$=$\frac{5}{2}$,△ABC的面积=10.
已知:一次函数y=-2x+10的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象相交于A,B两点(A在B的右侧).直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.$\frac{BC}{BD}$=$\frac{5}{2}$,△ABC的面积=10. 如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0).
如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0).