题目内容
10.我们规定,对于任意实数m,符号[m]表示小于或等于m的最大整数,例如:[2,1]=2,[2]=2,[-2,1]=-3,若对于整数x有[$\frac{3x-1}{2}$]=-5,则符合题意的x有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
分析 根据对于实数m我们规定[m]不大于m最大整数,可得答案.
解答 解:由x有[$\frac{3x-1}{2}$]=-5,
可得:$\left\{\begin{array}{l}{\frac{3x-1}{2}≥-5}\\{\frac{3x-1}{2}<-4}\end{array}\right.$,
解得:-3$≤x<-\frac{7}{3}$,
符合题意的x是-3.
故选B.
点评 本题考查了不等式组问题,利用[x]不大于x最大整数得出不等式组是解题关键.

练习册系列答案
相关题目
2.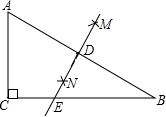 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )| A. | 2 | B. | $\frac{10}{3}$ | C. | $\frac{15}{8}$ | D. | $\frac{15}{2}$ |
19.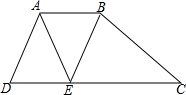 如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
 如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )| A. | $\sqrt{3}$ | B. | 11$\sqrt{3}$ | C. | 15$\sqrt{3}$ | D. | 22$\sqrt{3}$ |
20.点A(-1,2)与A′关于x轴对称,则点A′的坐标是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,-2) | D. | (-1,2) |
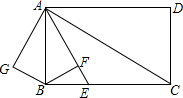 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.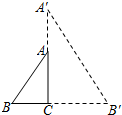 如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=$\frac{3}{5}$,现作如下操作:将△ACB沿直线AC翻折,然后再放大得到△A′CB′,联结A′B,如果△AA′B是等腰三角形,那么B′C的长是$\frac{27}{4}$. 已知,如图,点A、O、C在同一直线上,OE平分∠AOB,OF平分∠BOC.则∠EOF=90°.
已知,如图,点A、O、C在同一直线上,OE平分∠AOB,OF平分∠BOC.则∠EOF=90°.