题目内容
1.计算:(1)$\sqrt{64}$+$\frac{\root{3}{-27}}{2}$-$\sqrt{(-7)^{2}}$
(2)解方程$\left\{\begin{array}{l}{x-2y=5}\\{3x+y=1}\end{array}\right.$
(3)解方程$\left\{\begin{array}{l}{4b+a=15}\\{3a-4b=-3}\end{array}\right.$.
分析 (1)根据二次根式的性质化简即可;
(2)方程组利用代入消元法求出解即可;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)$\sqrt{64}$+$\frac{\root{3}{-27}}{2}$-$\sqrt{(-7)^{2}}$=8-$\frac{3}{2}$-7=-$\frac{1}{2}$;
(2)解:$\left\{\begin{array}{l}{x-2y=5①}\\{3x+y=1②}\end{array}\right.$,
由①得,x=5+2y③,
把③代入②得15+6y+y=1,
∴y=-2,
把y=-2代入③得,x=1,
∴$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
(3)$\left\{\begin{array}{l}{4b+a=15①}\\{3a-4b=-3②}\end{array}\right.$,
①+②得,4a=12,
∴a=3,
把a=3代入①得,b=3,
∴$\left\{\begin{array}{l}{a=3}\\{b=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.在平面直角坐标系中,点P的坐标为(0,2),点M的坐标为(m,-$\frac{3}{4}$m-3)(其中m为实数),当PM的长最小时,m的值为( )
| A. | -$\frac{12}{5}$ | B. | -$\frac{17}{5}$ | C. | -3 | D. | -4 |
12.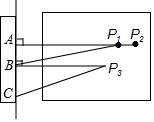 如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
 如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )| A. | 线段AP1的长 | B. | 线段AP2的长 | C. | 线段BP3的长 | D. | 线段CP3的长 |
11.顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 直角梯形 |