题目内容
4.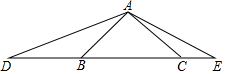 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2.
分析 将△ABE绕点A逆时针旋转90°,得到△ACF,证明△DAE≌△DAF,得到DF=DE,根据勾股定理计算即可.
解答 证明:∵∠DAE=135°,∠BAC=90°,AB=AC,
将△ABE绕点A逆时针旋转90°,得到△ACF,
则∠EAF=90°,BE=CF,∠ACF=∠ABE=45°,AE=AF,CF=BE,
∵∠DAE=135°,∠EAF=90°,
∴∠DAF=135°,
在△DAE和△DAF中,
$\left\{\begin{array}{l}{AD=AD}\\{∠DAE=∠DAF}\\{AE=AF}\end{array}\right.$,
∴△DAE≌△DAF,
∴DF=DE,
∠DCF=∠ACB+∠ACF=90°,
∴CD2+CF2=DF2.
∴CD2+BE2=DE2.
点评 本题考查的是勾股定理的应用、旋转变换的性质,掌握全等三角形的判定定理和性质定理、旋转变换的性质、勾股定理是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
19.若x<y,且(a+5)x>(a+5)y,则a的取值范围( )
| A. | a>-5 | B. | a≥-5 | C. | a<-5 | D. | a<5 |
9. 如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )
如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )
 如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )
如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
14.下列实数是无理数的是( )
| A. | -1 | B. | $\sqrt{3}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
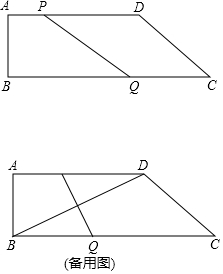 如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动.
如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动. 一运动员推铅球,铅球经过的路线为如图所示的抛物线.
一运动员推铅球,铅球经过的路线为如图所示的抛物线.