题目内容
16.已知y是关于x的一次函数,且点(0,-8),(1,2)在此函数图象上.(1)求这个一次函数表达式;
(2)若点(-2,y1),(2,y2)在此函数图象上,试比较y1,y2的大小;
(3)求当-3<y<3时x的取值范围.
分析 (1)由点的坐标利用待定系数法即可求出一次函数表达式;
(2)由一次项系数k=10>0即可得出一次函数y=10x-8为单调递增函数,结合-2<2即可得出y1<y2;
(3)将y=10x-8代入-3<y<3中即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)设该一次函数表达式为y=kx+b(k≠0),
将(0,-8)、(1,2)代入y=kx+b,
$\left\{\begin{array}{l}{b=-8}\\{k+b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=10}\\{b=-8}\end{array}\right.$,
∴该一次函数表达式为y=10x-8.
(2)∵在一次函数y=10x-8中k=10>0,
∴y随x的增大而增大.
∵-2<2,
∴y1<y2.
(3)当-3<y<3时,有-3<10x-8<3,
解得:0.5<x<1.1.
∴当-3<y<3时x的取值范围为0.5<x<1.1.
点评 本题考查了待定系数法求一次函数解析式、一次函数的性质以及解一元一次不等式,解题的关键是:(1)根据点的坐标利用待定系数法求出一次函数关系式;(2)根据k=10>0找出该一次函数为单调递增函数;(3)根据y的取值范围找出关于x的一元一次不等式.

练习册系列答案
相关题目
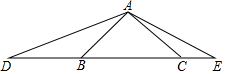 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2. 如图,沿△ABC的各边想同侧作正三角形ABD、BCF、ACE.
如图,沿△ABC的各边想同侧作正三角形ABD、BCF、ACE. 在矩形纸片ABCD中,AB=4,BC=10,E是AD边的中点,把矩形纸片沿过点E的直线折叠,使点A落在BC边上,则折痕EF的长为$\frac{5\sqrt{5}}{2}$.
在矩形纸片ABCD中,AB=4,BC=10,E是AD边的中点,把矩形纸片沿过点E的直线折叠,使点A落在BC边上,则折痕EF的长为$\frac{5\sqrt{5}}{2}$.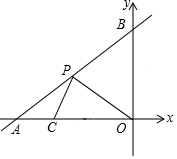 如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).
如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).