Question

15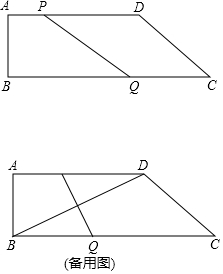．如图，在四边形ABCD中，AD‖BC，∠B=90°，AB=4cm，AD=8cm，BC=14cm，点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动，规定其中一个动点到达端点时，另一个端点也随之停止运动．
（1）t为何值时，PQ‖CD．
（2）t为何值时，PQ=CD．
（3）若P点的速度是$\frac{3}{2}$cm/s，其余条件不变，问Q点的速度是多少时，PQ垂直平分对角线BD？

Answer 1

分析 （1）由当PQ∥CD时，四边形PQCD为平行四边形，可得方程8-t=3t，解此方程即可求得答案；
（2）根据PQ=CD，一种情况是：四边形PQCD为平行四边形，可得方程8-t=3t，一种情况是：四边形PQCD为等腰梯形，可求得当QC-PD=QC-EF=QF+EC=2CE，即3t-（8-t）=12时，四边形PQCD为等腰梯形，解此方程即可求得答案；
（3）当PQ垂直平分对角线BD时，得出四边形BQDP是菱形，得出BQ=BP=PD=8-$\frac{3}{2}$t，在Rt△ABP中，由勾股定理得出方程，解方程求出t的值，得出BQ=5，求出CQ=9，即可得出Q点的速度．

解答 解：设运动时间为ts，根据题意得：PA=t，CQ=3t，
则PD=AD-PA=8-t．
（1）∵AD∥BC，
即PQ∥CD，
∴当PD=CQ时，四边形PQCD为平行四边形，
即8-t=3t，
解得：t=2，
即当t=2时，PQ∥CD；
（2）若PQ=DC，分两种情况：
①PQ=DC，则四边形PQCD是平行四边形，由（1）可知，t=2，
②PQ=DC，则四边形PQCD是等腰梯形，则QC=PD+2（BC-AD），
可得方程：3t=8-t+12，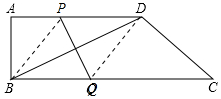
解得：t=5；
综上所述：t为2s或5s时，PQ=CD．
（3）当PQ垂直平分对角线BD时，连接BP，DQ，
∵PD∥BC，
∴四边形BQDP是菱形，
∴BQ=BP=PD=8-$\frac{3}{2}$t，
在Rt△ABP中，AP=$\frac{3}{2}$t，AB=4，
由勾股定理得：4²+（$\frac{3}{2}$t）²=（8-$\frac{3}{2}$t）²，
解得：t=2，
∴BQ=8-$\frac{3}{2}$×2=5，
∴CQ=14-5=9，
∴Q点的速度=9÷2=4.5（cm/s），
即Q点的速度是4.5cm/s时，PQ垂直平分对角线BD．

点评 此题是四边形综合题目，考查了直角梯形的性质、平行四边形的判定、等腰梯形的判定以及全等三角形的判定与性质．此题综合性强，有一定难度，注意掌握数形结合思想与分类讨论思想的应用．