题目内容
12. 一运动员推铅球,铅球经过的路线为如图所示的抛物线.
一运动员推铅球,铅球经过的路线为如图所示的抛物线.(1)求铅球所经过的路线的函数表达式和自变量的取值范围;
(2)求铅球落地点离运动员有多远(精确到0.01)?
分析 (1)利用顶点式设抛物线的解析式为y=a(x-4)2+3,把(0,$\frac{3}{2}$)代入得到a=-$\frac{3}{32}$,由此即可解决问题.
(2)令y=0,解方程即可解决问题.
解答 解:(1)由题意设抛物线的解析式为y=a(x-4)2+3,
把(0,$\frac{3}{2}$)代入得到a=-$\frac{3}{32}$,
∴抛物线的解析式为y=-$\frac{3}{32}$(x-4)2+3(0<x≤4+4$\sqrt{2}$).
(2)令y=0,得到-$\frac{3}{32}$(x-4)2+3=0,解得x=4+4$\sqrt{2}$或4-4$\sqrt{2}$(舍弃),
∴铅球落地点离运动员有4+4$\sqrt{2}$≈9.66m.
点评 本题考查二次函数的应用,解题的关键是熟练掌握二次函数的三种形式,学会利用待定系数法确定函数解析式,属于中考常考题型.

练习册系列答案
相关题目
2.已知|x|=2,|y|=4,且x>y,则x-y的值为( )
| A. | 6 | B. | 6或2 | C. | ±6或±2 | D. | -2或-6 |
20.旭日商场销售A,B两种品牌的钢琴,这两种钢琴的进价和售价如下表所示:
该商场计划购进两种钢琴若干套,共需66万元,全部销售后可获毛利润9万元.(毛利润=(售价-进价)×销售量)
(1)该商场计划购进A,B两种品牌的钢琴各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种钢琴的购进数量,增加B种钢琴的购进数量,已知B种钢琴增加的数量是A种钢琴减少数量的1.5倍,若用于购进这两种钢琴的总资金不超过69万元,问A种钢琴购进数量至多减少多少套?
| A | B | |
| 进价(万元/.套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的钢琴各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种钢琴的购进数量,增加B种钢琴的购进数量,已知B种钢琴增加的数量是A种钢琴减少数量的1.5倍,若用于购进这两种钢琴的总资金不超过69万元,问A种钢琴购进数量至多减少多少套?
17.y关于x的一次函数y=2x+m2+1的图象不可能经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE||BC,DE交AF于点G,设AD=5,AB=15,AC=12,GF=6.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE||BC,DE交AF于点G,设AD=5,AB=15,AC=12,GF=6.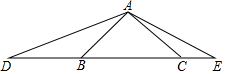 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°,求证:CD2+BE2=DE2. 如图,沿△ABC的各边想同侧作正三角形ABD、BCF、ACE.
如图,沿△ABC的各边想同侧作正三角形ABD、BCF、ACE.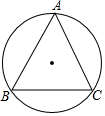 如图,△ABC中,BC=5,sinA=$\frac{3}{5}$
如图,△ABC中,BC=5,sinA=$\frac{3}{5}$