题目内容
15.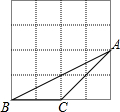 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
分析 根据勾股定理,可得AB,AC的长,根据三角形的面积公式,可得CD的长,再根据勾股定理,可得AD的长,根据锐角三角函数的余弦等于邻边比斜边,可得答案.
解答 解:如图,作CD⊥AB于D点,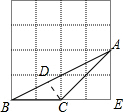 ,
,
由勾股定理,得
AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=2$\sqrt{5}$,AC=$\sqrt{C{E}^{2}+A{E}^{2}}$=2$\sqrt{2}$,
由三角形的面积公式,得
$\frac{1}{2}$AB•DC=$\frac{1}{2}$BC•AE,
即DC=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
由勾股定理,得
AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{8-\frac{4}{5}}$=$\frac{6\sqrt{5}}{5}$,
cos∠BAC=$\frac{AD}{AC}$=$\frac{\frac{6\sqrt{5}}{5}}{2\sqrt{2}}$=$\frac{3\sqrt{10}}{10}$,
故选:D.
点评 本题考查了锐角三角函数的定义,利用了勾股定理,锐角三角函数的定义.

练习册系列答案
相关题目
5.顺次连结矩形四边的中点所得的四边形是( )
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 以上都不对 |
3.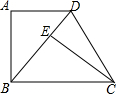 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
10.已知0≤x≤$\frac{3}{2}$,则函数y=x2+x+1( )
| A. | 有最小值$\frac{3}{4}$,但无最大值 | B. | 有最小值$\frac{3}{4}$,有最大值1 | ||
| C. | 有最小值1,有最大值$\frac{19}{4}$ | D. | 无最小值,也无最大值 |
7.对二次函数y=3x2-6x的图象性质,下列说法不正确的是( )
| A. | 开口向上 | B. | 对称轴为x=1 | C. | 顶点坐标为(1,-3) | D. | 最小值为3 |
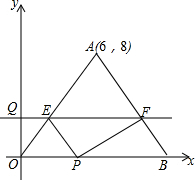 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0). 一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于x的方程kx+b=-3的解为x=-4.
一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于x的方程kx+b=-3的解为x=-4.