题目内容
20．
一次函数y=kx+b（k、b为常数，且k≠0）的图象如图所示．根据图象信息可求得关于x的方程kx+b=-3的解为x=-4．
分析 先根据一次函数y=kx+b过（2，3），（0，1）点，求出一次函数的解析式，再解关于x的方程kx+b=-3，即可求出答案．
解答 解∵一次函数y=kx+b过（2，3），（0，1）点，
∴$\left\{\begin{array}{l}{2k+b=3}\\{b=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$，
一次函数的解析式为：y=x+1，
解方程x+1=-3，得x=-4．
故答案为：x=-4．
点评 本题考查了一次函数与一元一次方程，待定系数法求一次函数的解析式，一元一次方程的解法．求出k与b的值是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，跷跷板AB的支柱OD经过它的中点O，且垂直于地面BC，垂足为D，OD=50cm，当它的一端B着地时，另一端A离地面的高度AC为100cm．
8．
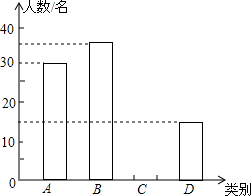由于各地雾霾天气越来越严重，2015年春节前夕，蚌埠市某校团委向全校3000名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A类：不放烟花爆竹；B类：少放烟花爆竹；C类：不会减少烟花爆竹数量；D类：使用电子鞭炮”四个选项对100名学生进行问卷调查，并将调查结果绘制成如下两幅统计图表（不完整），请根据图表，回答下列问题：
（1）表格中a=30，b=15，并补全条形统计图；
（2）如果绘制扇形统计图，请求出C类所占的圆心角的度数；
（3）根据抽样结果，请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名？
由于各地雾霾天气越来越严重，2015年春节前夕，蚌埠市某校团委向全校3000名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A类：不放烟花爆竹；B类：少放烟花爆竹；C类：不会减少烟花爆竹数量；D类：使用电子鞭炮”四个选项对100名学生进行问卷调查，并将调查结果绘制成如下两幅统计图表（不完整），请根据图表，回答下列问题：| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
（2）如果绘制扇形统计图，请求出C类所占的圆心角的度数；
（3）根据抽样结果，请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名？
15．
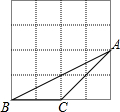如图，△ABC的顶点都在边长相等的小正方形的顶点上，则cos∠BAC等于（ ）
如图，△ABC的顶点都在边长相等的小正方形的顶点上，则cos∠BAC等于（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{10}}}{5}$ | C． | $\frac{{\sqrt{10}}}{10}$ | D． | $\frac{{3\sqrt{10}}}{10}$ |
已知，如图，直线MN交⊙O于A，B两点，AC是⊙O的直径，DE切⊙O于点D，且DE⊥MN于点E．
如图，已知直线y=kx-3经过点M，求此直线上