题目内容
5.顺次连结矩形四边的中点所得的四边形是( )| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 以上都不对 |
分析 因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
解答 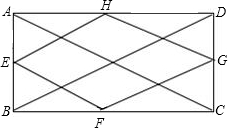 解:连接AC、BD,
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=$\frac{1}{2}$BD,
同理FG=$\frac{1}{2}$BD,HG=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
点评 本题考查了菱形的判定,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
相关题目
16.下列实数:$\frac{π}{3}$,$\frac{22}{7}$,0.414,$\root{3}{9}$,$\sqrt{36}$,$\sqrt{2}$,2.12112111211112…(相邻两个2之间依次多1),其中无理数个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.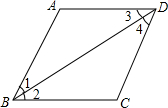 下列条件中,能说明AD∥BC的条件有( )个
下列条件中,能说明AD∥BC的条件有( )个
①∠1=∠4 ②∠2=∠3 ③∠1+∠2=∠3+∠4
④∠A+∠C=180° ⑤∠A+∠ABC=180° ⑥∠A+∠ADC=180°.
 下列条件中,能说明AD∥BC的条件有( )个
下列条件中,能说明AD∥BC的条件有( )个①∠1=∠4 ②∠2=∠3 ③∠1+∠2=∠3+∠4
④∠A+∠C=180° ⑤∠A+∠ABC=180° ⑥∠A+∠ADC=180°.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.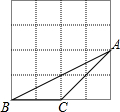 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
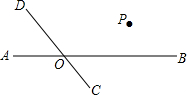 如图,直线CD与直线AB相交于O,根据下列语句画图:
如图,直线CD与直线AB相交于O,根据下列语句画图: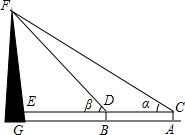 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).