题目内容
10.已知0≤x≤$\frac{3}{2}$,则函数y=x2+x+1( )| A. | 有最小值$\frac{3}{4}$,但无最大值 | B. | 有最小值$\frac{3}{4}$,有最大值1 | ||
| C. | 有最小值1,有最大值$\frac{19}{4}$ | D. | 无最小值,也无最大值 |
分析 先求得函数图象的对称轴,根据抛物线的开口方向和抛物线的增减性进行解答.
解答 解:∵y=x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$.
∴该函数图象的对称轴是x=-$\frac{1}{2}$,在0≤x≤$\frac{3}{2}$上,y随x的增大而增大,
∴当x=0时,y最小=1;
当x=$\frac{3}{2}$时,y最大=$\frac{19}{4}$.
故选:C.
点评 本题考查了二次函数的最值.确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需要( )张?


| A. | 15 | B. | 16 | C. | 21 | D. | 22 |
15.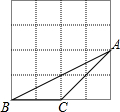 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
 如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
 解不等式3(x+1)-6≤4x,并把解集在数轴上表示出来.
解不等式3(x+1)-6≤4x,并把解集在数轴上表示出来.