题目内容
4.已知O是?ABCD的对角线交点,△AOB的面积为5cm2,求?ABCD的面积.分析 由平行四边形的对角线互相平分得出△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积,即可求出?ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积=5cm2,
∴?ABCD的面积=4×5cm2=20cm2.
点评 本题考查了平行四边形的性质以及面积的计算方法;熟练掌握平行四边形的性质,得出△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积是解决问题的关键.

练习册系列答案
相关题目
15.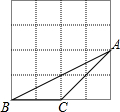 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
16.若x、y为有理数,且m=2x2+9y2+8x-12y+12,则m的值为( )
| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 0 |
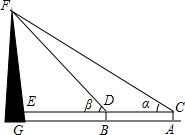 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米). 如图,已知直线y=kx-3经过点M,求此直线上
如图,已知直线y=kx-3经过点M,求此直线上