题目内容
3.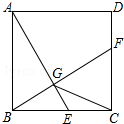 如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:
如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为$\frac{π}{4}$;④CG的最小值为$\frac{\sqrt{5}}{2}$-1.
其中正确的说法是②③.(把你认为正确的说法的序号都填上)
分析 根据正方形对角线的性质可得出当E移动到与C重合时,F点和D点重合,此时G点为AC中点,故①错误;
求得∠BAE=∠CBF,根据正方形的性质可得AB=BC,∠ABC=∠C=90°,然后利用“角角边”证明△ABE和△BCF全等,根据全等三角形对应角相等可得AE=BF,判断出②正确;
根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,然后求出弧的长度,判断出③正确;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,根据勾股定理求出最小CG长度.
解答 解:∵在正方形ABCD中,BF⊥AE,
∴∠AGB保持90°不变,
∴G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,
∴当E移动到与C重合时,F点和D点重合,此时G点为AC中点,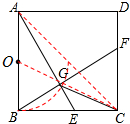
∴AG=GE,故①错误;
∵BF⊥AE,
∴∠AEB+∠CBF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠BAE=∠CBF}\\{∠ABE=∠BCF=90°}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴故②正确;
∵当E点运动到C点时停止,
∴点G运动的轨迹为$\frac{1}{4}$圆,
圆弧的长=$\frac{1}{4}$×π×1=$\frac{π}{4}$,故③正确;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,
OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{\frac{1}{4}+{1}^{2}}$=$\frac{\sqrt{5}}{2}$,
CG的最小值为OC-OG=$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$,故④错误;
综上所述,正确的结论有②③.
故答案为②③.
点评 本题考查了四边形综合题,其中涉及到了正方形的性质,全等三角形的判定与性质,弧长的计算,勾股定理的应用,熟记性质并求出△ABE和△BCF全等是解题的关键,用阿拉伯数字加弧线表示角更形象直观.

| A. | x3+x3=x6 | B. | x4÷x2=x2 | C. | (m5)5=m10 | D. | x2y3=(xy)3 |
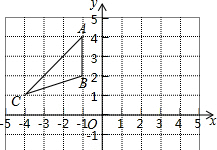 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点C的对应点C′的坐标为( )
已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点C的对应点C′的坐标为( )| A. | (-4,1) | B. | (-4,-1) | C. | (4,-1) | D. | (4,1) |
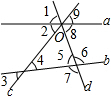 如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题. 如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0).
如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0). 如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.
如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.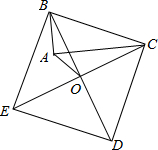 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.