题目内容
5.解下列方程组:(1)用代入法解方程组$\left\{\begin{array}{l}{x+3y=-1}\\{3x-2y=8}\end{array}\right.$
(2)用加减法解方程组$\left\{\begin{array}{l}{\frac{x+2}{3}+\frac{y+1}{2}=2}\\{\frac{x+2}{3}+\frac{1-y}{2}=1}\end{array}\right.$
(3)解方程组$\left\{\begin{array}{l}{2x+3y+z=6}\\{x-y+2z=-1}\\{x+2y-z=5}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可.
(2)首先把原方程变形为$\left\{\begin{array}{l}{2x+3y=5①}\\{2x-3y=-1②}\end{array}\right.$,然后用①+②,可消去未知数y,解出x的值,再把x的值代入式子①,即可得到y的值.
(3)利用加减法消掉一个未知数,将三元一次方程组转化为二元一次方程组,再进行解答.
解答 解:(1)$\left\{\begin{array}{l}{x+3y=-1①}\\{3x-2y=8②}\end{array}\right.$,
由①得:x=-3y-1③,
把③代入②得:-9y-3-2y=8,
解得:y=-1,
将y=-1代入③得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
(2)原方程变形为$\left\{\begin{array}{l}{2x+3y=5①}\\{2x-3y=-1②}\end{array}\right.$,
①+②得:4x=4,
x=1,
把x=1代入①得:2+3y=5,
y=1,
∴方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{2x+3y+z=6①}\\{x-y+2z=-1②}\\{x+2y-z=5③}\end{array}\right.$
③+①得,3x+5y=11④,
③×2+②得,3x+3y=9⑤,
④-⑤得2y=2,y=1,
将y=1代入⑤得,3x=6,
x=2,
将x=2,y=1代入①得,z=6-2×2-3×1=-1,
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$.
点评 本题考查了解二元一次方程组和解三元一次方程组,解题的关键是消元,消元的方法有两种:①加减法消元,②代入法消元.当系数成倍数关系时,一般用加减法消元,系数为1时,一般用代入法消元.

| A. | x3+x3=x6 | B. | x4÷x2=x2 | C. | (m5)5=m10 | D. | x2y3=(xy)3 |
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | y=$\frac{1}{2}$(x-4)2-4 | B. | y=$\frac{1}{2}$x2 | C. | y=$\frac{1}{2}$(x-7)2-4 | D. | y=$\frac{1}{2}$(x-1)2-4 |
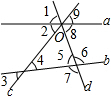 如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.