题目内容
12．等腰三角形的周长为16cm，底边长为x cm，腰长为y cm，则x与y之间的关系式为y=8-$\frac{1}{2}$x（0＜x＜8）．分析 根据三角形周长公式可写出y与x的函数关系式，注意用三角形三边关系表示出x的取值范围．
解答 解：∵等腰三角形的周长为16cm，底边长为x cm，腰长为y cm．
∴x+2y=16，
∴y=8-$\frac{1}{2}$x（0＜x＜8）．
故答案为：y=8-$\frac{1}{2}$x（0＜x＜8）．
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3．
如图，△ABC的角平分线相交于点P，∠BPC=125°，则∠A的度数为（ ）
如图，△ABC的角平分线相交于点P，∠BPC=125°，则∠A的度数为（ ）| A． | 60° | B． | 65° | C． | 70° | D． | 75° |
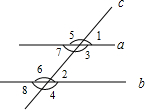如图，直线a、b都与直线c相交，给出下列条件：①∠1=∠2； ②∠3=∠6；③∠1=∠4；④∠5+∠8=180°，其中能判断a∥b的条件是：①②④．（把你认为正确的序号填在空格内）
7．
如图所示，a∥b，∠2是∠1的3倍，则∠2等于（ ）
如图所示，a∥b，∠2是∠1的3倍，则∠2等于（ ）| A． | 150° | B． | 135° | C． | 90° | D． | 45° |
如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为M，若∠1=50°，则∠2=40°．
2．
实数a、b在数轴上的位置如图，则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$的结果是（ ）
实数a、b在数轴上的位置如图，则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$的结果是（ ）| A． | -2b | B． | -2a | C． | 2b-2a | D． | 0 |