题目内容
3. 如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )
如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
分析 先根据三角形内角和定理求出∠1+∠2的度数,再根据角平分线的性质求出∠ABC+∠ACB的度数,由三角形内角和定理即可求出答案.
解答 解:∠1+∠2+∠BPC=180°(三角形内角和等于180°),
∵∠BPC=125°,
∴∠1+∠2=55°,
∵BP、CP是角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
∴∠ABC+∠ACB=110°,
∵∠ABC+∠ACB+∠A=180°,
∴∠A=70°.
故选C.
点评 本题考查的是三角形内角和定理及角平分线的性质,属较简单题目.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.7的倒数是( )
| A. | 7 | B. | -7 | C. | $\frac{1}{7}$ | D. | -$\frac{1}{7}$ |
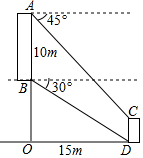 如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)
如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)


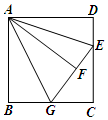 如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.
如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.