题目内容
2. 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )| A. | -2b | B. | -2a | C. | 2b-2a | D. | 0 |
分析 根据数轴上点的位置关系,可得1>b>0>a>-1,根据二次根式的性质,绝对值的性质,可得答案.
解答 解:由数轴上点的位置关系,得
1>b>0>a>-1,
所以$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$
=-a-b-(b-a)
=-a-b-b+a
=-2b,
故选A.
点评 本题考查了实数与数轴,利用数轴上点的位置关系得出1>b>0>a>-1是解题关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
14.5的相反数是( )
| A. | 2 | B. | -5 | C. | 5 | D. | $\frac{1}{5}$ |
7.设某数为x,如果比它的$\frac{3}{4}$大1的数的相反数是5,则可以列出方程( )
| A. | -($\frac{3}{4}$x+1)=5 | B. | -$\frac{3}{4}$x+1=5 | C. | $\frac{3}{4}$x-1=5 | D. | -x($\frac{3}{4}$x+1)=5 |
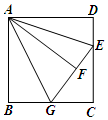 如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.
如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.