题目内容
3.已知正方形ABCD和正方形CEFG,连结AF交BC于点O,点P是AF的中点,过点P作PH⊥DG于H,CD=2,CG=1.(1)如图1,点D、C、G在同一直线上,点E在BC边上,求PH的长;
(2)把正方形CEFG绕着点C逆时针旋转α(0°<α<180°)
①如图2,当点E落在AF上时,求CO的长;
②如图3,当DG=$\sqrt{7}$时,求PH的长.

分析 (1)先判断出四边形APGF是梯形,再判断出PH是梯形的中位线,得到PH=$\frac{1}{2}$(fg+ad);
(2)①先判断出△COE∽△AOB,得到AO是CO的2倍,设出CO,表示出BO,AO,再用勾股定理计算,②先找出辅助线,再判断出△ARD≌△DSC,△CSG≌△GTF,求出AR+FT,最后用梯形中位线即可.
解答 解:(1)PH⊥CD,AD⊥CD,
∴PH∥AD∥FG,
∵点P是AF的中点,
∴PH是梯形APGF的中位线,
∴PH=$\frac{1}{2}$(FG+AD)=$\frac{3}{2}$,
(2)①∵∠CEO=∠B=90°,∠COE=∠AOB,
∴△COE∽△AOB,
∴$\frac{CO}{AO}=\frac{CE}{AB}$,
∴$\frac{CO}{AO}=\frac{1}{2}$,
设CO=x,
∴AO=2x,BO=2-x,
在△ABO中,根据勾股定理得,4+(2-x)2=(2x)2,
∴x=$\frac{2\sqrt{7}-2}{3}$或x=$\frac{-2\sqrt{7}-2}{3}$(舍),
∴CO=x=$\frac{2\sqrt{7}-2}{3}$.
②如图3,
分别过点A,C,F作直线DG的垂线,垂足分别为R,S,T,
∵∠ADR+∠CDS=90°,∠CDS+∠DCS=90°,
∴∠ADR=∠DCS,
∵∠ADR=∠CSD=90°,
∵AD=CD
∴△ARD≌△DSC,
∴AR=DS,
同理:△CSG≌△GTF,
∴SG=FT,
∴AR+FT=DS+SG=DG=$\sqrt{7}$,
同(1)的方法得,PH是梯形ARTF的中位线,
∴PH=$\frac{1}{2}$(AR+FT)=$\frac{\sqrt{7}}{2}$.
点评 此题是四边形综合题,主要考查了梯形的中位线的求法,三角形全等的判定和性质,解本题的关键是构造出梯形,难点是作辅助线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案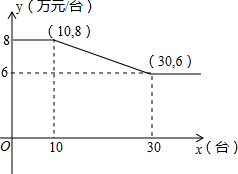 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示. 已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h).
已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h).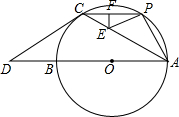 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA. 如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.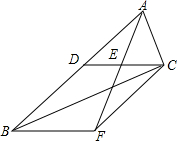 如图,四边形BFCD为平行四边形,点E是AF的中点.
如图,四边形BFCD为平行四边形,点E是AF的中点.
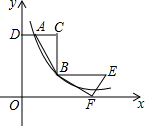 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.