题目内容
8. 如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
分析 由点A在直线y=-2x上且A点纵坐标为2求得点A坐标,将点A、B坐标代入y=kx+b,求出待定系数k、b的值即可.
解答 解:在函数y=-2x中令y=2得:-2x=2,
解得:x=-1,
∴点A坐标为(-1,2),
将点A(-1,2)、点B(1,0)代入y=kx+b,得:
$\left\{\begin{array}{l}{-k+b=2}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
∴一次函数解析式为:y=-x+1.
点评 本题主要考查待定系数法求一次函数解析式,根据题意求得点A、B坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
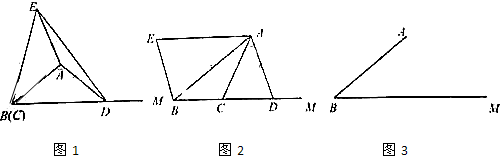
16. 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )| A. | (2$\sqrt{3}$,30°) | B. | (60°,2$\sqrt{3}$) | C. | (30°,4) | D. | (30°,2$\sqrt{3}$) |
 如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若
如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若
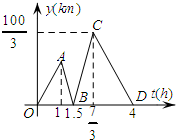 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题: