题目内容
13.已知a,b满足$\sqrt{4a-5b}$+$\sqrt{a-b-1}$=0,求$\sqrt{ab}$$÷\sqrt{\frac{{b}^{3}}{a}}$的值.分析 根据非负数的性质列出二元一次方程组,求出a、b的值,根据二次根式的除法法则把原式化简,代入计算即可.
解答 解:由题意得,4a-5b=0,a-b-1=0,
则$\left\{\begin{array}{l}{4a-5b=0}\\{a-b=1}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$,
则$\sqrt{ab}$$÷\sqrt{\frac{{b}^{3}}{a}}$=$\sqrt{ab×\frac{a}{{b}^{3}}}$=$\frac{a}{b}$,
当a=5,b=4时,原式=$\frac{5}{4}$.
点评 本题考查的是非负数的性质和二次根式的混合运算,掌握非负数之和等于0时,各项都等于0是解题的关键,注意分式的混合运算法则的灵活运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
6.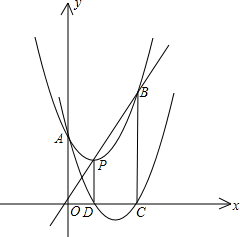 如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )
如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )
 如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )
如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )| A. | 平行四边形 | B. | 正方形 | C. | 菱形 | D. | 矩形 |
1.函数y=kx+b图象经过一、三、四象限,则函数y=bx-k图象经过( )
| A. | 一、二、四象限 | B. | 一、二、三象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
5.已知(a-2)2+$\sqrt{b+3}$=0,则P(-a,-b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |