题目内容
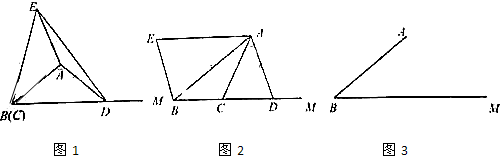
12.已知△ABC是边长为a的等边三角形,D、E、F分别是AB、AC和BC边上的点.如图①,当$\frac{AD}{AB}$=$\frac{BF}{BC}$=$\frac{CE}{CA}$=$\frac{1}{2}$时,$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=$\frac{1}{4}$.
(1)如图②,当$\frac{AD}{AB}$=$\frac{BF}{BC}$=$\frac{CE}{CA}$=$\frac{1}{3}$时,求$\frac{{S}_{△DEF}}{{S}_{△ABC}}$;
(2)如图③,当$\frac{AD}{AB}$=$\frac{BF}{BC}$=$\frac{CE}{CA}$=$\frac{1}{4}$时,求$\frac{{S}_{△DEF}}{{S}_{△ABC}}$;
(3)猜想:当$\frac{AD}{AB}$=$\frac{BF}{BC}$=$\frac{CE}{CA}$=$\frac{1}{n}$时,求$\frac{{S}_{△DEF}}{{S}_{△ABC}}$的值是多少?直接写出结果(用代数式表示)
分析 (1)如图②中,作AM⊥BC于M,DF′⊥BC于F′,易证△DBF≌△FCE≌△EAD,设BC=3a,求出△BDF面积,△DEF面积即可解决问题.
(2)如图②中,作AM⊥BC于M,DN⊥BC于N.设BC=4a,求出△BDF面积,△DEF面积即可解决问题.
(3)如图②中,作AM⊥BC于M,DN⊥BC于N.设BC=na,求出△BDF面积,△DEF面积即可解决问题.
解答 解:(1)如图 ②中,作AM⊥BC于M,DF′⊥BC于F′,设BC=3a,
②中,作AM⊥BC于M,DF′⊥BC于F′,设BC=3a,
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=∠BAC=60°
∵$\frac{AD}{AB}$=$\frac{BF}{BC}$=$\frac{CE}{CA}$=$\frac{1}{3}$,
∴AD=BF=CE=a,BD=CF=AE=2a,
∴△DBF≌△FCE≌△EAD,
∴S△DBF=S△ECF=S△ADE,
在RT△BDF′中,∵∠DF′B=90°,∠B=60°,
∴BF′=$\frac{1}{2}$BD=a,DF=$\sqrt{3}$a,
∴BF=BF′=a,
∴F、F′共点.
∴S△DBF=$\frac{1}{2}$•a•$\sqrt{3}$a=$\frac{\sqrt{3}}{2}$a2,
∴S△DEF=S△ABC-3S△BDF=$\frac{3\sqrt{3}}{4}$a2,
∴$\frac{{S}_{△EDF}}{{S}_{△ABC}}$=$\frac{\frac{3\sqrt{3}}{4}{a}^{2}}{\frac{9\sqrt{3}}{4}{a}^{2}}$=$\frac{1}{3}$.
(2) 如图②中,作AM⊥BC于M,DN⊥BC于N.设BC=4a则BD=CF=AE=3a,AD=BF=CE=a,S△ABC=4$\sqrt{3}$a2,
如图②中,作AM⊥BC于M,DN⊥BC于N.设BC=4a则BD=CF=AE=3a,AD=BF=CE=a,S△ABC=4$\sqrt{3}$a2,
∵DN∥AM,
∴$\frac{DN}{AM}$=$\frac{BD}{BA}$=$\frac{3}{4}$,
∴DN=$\frac{3\sqrt{3}}{2}$a,
∴S△BDF=$\frac{1}{2}$•a•$\frac{3\sqrt{3}}{2}$a=$\frac{3\sqrt{3}}{4}$a2
由(1)可知S△DEF=S△ABC-3S△BDF=$\frac{7\sqrt{3}}{4}$a2,
∴$\frac{{S}_{△EDF}}{{S}_{△ABC}}$=$\frac{7}{16}$.
(3)如图③中,设BC=na,则BD=CF=AE=n-1,AD=BF=CE=a,DN=$\frac{(n-1)a}{2}\sqrt{3}$,
∴S△BDF=$\frac{1}{2}$•a•$\frac{(n-1)a}{2}\sqrt{3}$=$\frac{(n-1){a}^{2}}{4}$$\sqrt{3}$,
∴S△DEF=$\frac{\sqrt{3}}{4}$n2a2-$\frac{3(n-1){a}^{2}}{4}$$\sqrt{3}$,
∴$\frac{{S}_{△EDF}}{{S}_{△ABC}}$=$\frac{{n}^{2}-3n+3}{{n}^{2}}$.
点评 本题考查等边三角形的性质、相似三角形的判定和性质、平行线分线段成比例定理、三角形面积等知识,解题的关键巧妙是设未知数,求出相应三角形面积,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | mt2>nt2 | B. | mt2≥nt2 | C. | mt>nt | D. | mt<nt |



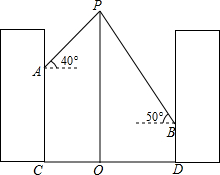 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)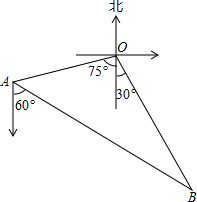 如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?
如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?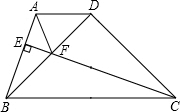 如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.