题目内容
6.已知二次函数y=(x-1)2-4的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,顶点为D.(1)求点A,B,C,D的坐标.并画出该二次函数的大致图象;
(2)说出抛物线y=(x-1)2-4可由抛物线y=x2如何平移得到;
(3)求四边形BOCD的面积.
分析 (1)令y=0可以求得A、B坐标,令x=0可以求得点C坐标,根据顶点式可以直径写出顶点坐标.
(2)观察图象即可解决问题.
(3)根据S四边形CDBO=S△OCD+S△OBD计算即可.
解答 解:(1)令y=0,(x-1)2-4=0,解得x=3或-1,得A(-1,0),B(3,0),
令x=0,y=-3,得C(0,-3),顶点D(1,-4).
图象如图所示,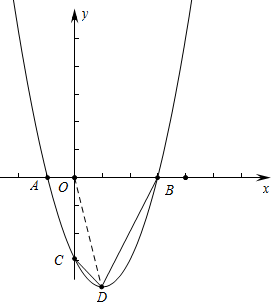
(2)把抛物线y=x2抛向右平移1个单位,再向下平移4个单位得到抛物线y=(x-1)2-4.
(3)连接OD,S四边形CDBO=S△OCD+S△OBD=$\frac{1}{2}$•3•1+$\frac{1}{2}$•3•4=$\frac{15}{2}$.
点评 本题考查二次函数与x轴交点、二次函数的性质等知识,解题的关键是熟练掌握求抛物线与坐标轴的交点,学会利用分割法求四边形面积,属于中考常考题型.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
16.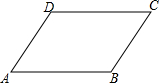 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |

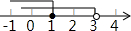
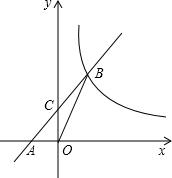 如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.
如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.