题目内容
18．
如图，AB∥CD，点E在BC上，且DE⊥BC，∠D=58°，则∠B的度数为（ ）| A． | 32° | B． | 42° | C． | 52° | D． | 58° |
分析 在Rt△DEC中可求得∠C，再利用平行线的性质可求得∠B．
解答 解：
∵DE⊥BC，
∴∠DEC=90°，
∴∠C=90°-∠D=90°-58°=32°，
∵AB∥CD，
∴∠B=∠C=32°，
故选A．
点评 本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补．
练习册系列答案
星级口算天天练系列答案
相关题目
9．下列定理有逆定理的是（ ）
| A． | 全等三角形的对应角相等 | |
| B． | 如果两个角都是45°，那么这两个角相等 | |
| C． | 两直线平行，同位角相等 | |
| D． | 对顶角相等 |
3．
如图，在矩形ABCD中，∠BOC=120°，AB=5，则BD的长为（ ）
如图，在矩形ABCD中，∠BOC=120°，AB=5，则BD的长为（ ）| A． | 5 | B． | 10 | C． | 12 | D． | 13 |
7．
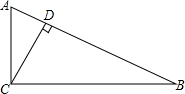如图，在△ABC中，∠ACB=90°，CD为高，AC=4，则下列计算结果错误的是（ ）
如图，在△ABC中，∠ACB=90°，CD为高，AC=4，则下列计算结果错误的是（ ）| A． | 若BC=3，则CD=2.4 | B． | 若∠A=30°，则BD=$\frac{\sqrt{3}}{3}$ | ||
| C． | 若∠A=45°，则AD=2$\sqrt{2}$ | D． | 若BC=2，则S△ADC=$\frac{16}{5}$ |
