题目内容
10.平行四边形ABCD的对角线AC、BD相交于点O,若AC+BD=24厘米,△OAB的周长是18厘米,则AB=6厘米.分析 首先由?ABCD的对角线AC,BD相交于点O,求得OA=$\frac{1}{2}$AB,OB=$\frac{1}{2}$BD,又由AC+BD=24厘米,可求得OA+OB的长,继而求得AB的长.
解答 解:∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,
∵AC+BD=24厘米,
∴OA+OB=12厘米,
∵△OAB的周长是18厘米,
∴AB=6厘米.
故答案为:6.
点评 此题考查了平行四边形的性质.注意掌握平行四边形的对角线互相平分定理的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.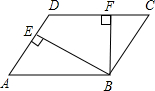 如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
 如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )| A. | 75° | B. | 60° | C. | 50° | D. | 45° |
18. 如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
 如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )| A. | 32° | B. | 42° | C. | 52° | D. | 58° |
2. 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )| A. | $\sqrt{2}$ | B. | 1.5 | C. | $\sqrt{3}$ | D. | 2 |
19. 如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
 如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )| A. | 8 | B. | $8\sqrt{3}$ | C. | $12\sqrt{3}$ | D. | $16\sqrt{3}$ |
7.对角线互相垂直平分且相等的四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
 在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
在?ABCD中,点E、F是对角线AC上两点,且AE=CF. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为$\frac{24}{5}$cm.
如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为$\frac{24}{5}$cm.