题目内容
7.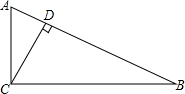 如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )
如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )| A. | 若BC=3,则CD=2.4 | B. | 若∠A=30°,则BD=$\frac{\sqrt{3}}{3}$ | ||
| C. | 若∠A=45°,则AD=2$\sqrt{2}$ | D. | 若BC=2,则S△ADC=$\frac{16}{5}$ |
分析 根据勾股定理、直角三角形的性质、直角三角形的面积进行计算即可.
解答 解:A、若BC=3,则CD=2.4,故正确;
B、若∠A=30°,则BD=2$\sqrt{5}$-2$\sqrt{3}$,故错误;
C、若∠A=45°,则AD=2$\sqrt{2}$,故正确;
D、若BC=2,则S△ADC=$\frac{16}{5}$,故正确;
故选B.
点评 本题考查了三角形的面积和30°角的直角三角形的性质,在直角三角形中,若一个角等于30度,则它所对的直角边等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.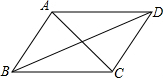 如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
 如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )| A. | $\overrightarrow{BA}$+$\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CB}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$ |
18. 如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
 如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且DE⊥BC,∠D=58°,则∠B的度数为( )| A. | 32° | B. | 42° | C. | 52° | D. | 58° |
2. 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )| A. | $\sqrt{2}$ | B. | 1.5 | C. | $\sqrt{3}$ | D. | 2 |
19. 如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
 如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )
如图,菱形ABCD的周长为32,∠C=120°,AE⊥BC,AF⊥CD,垂足为别为E、F,连结EF,则△AEF的面积是( )| A. | 8 | B. | $8\sqrt{3}$ | C. | $12\sqrt{3}$ | D. | $16\sqrt{3}$ |
 填空:
填空: 如图,AB交CD于O,OE⊥AB.
如图,AB交CD于O,OE⊥AB.