题目内容
某班同学去春游花了250元包租了一辆客车,如果参加春游的同学每人交8元钱租车费,还不够,如果每人交9元,还用不了.用不等式表示出上述问题中存在的不等关系.
 见解析
【解析】试题分析:根据每人交8元钱租车费,还不够可得8x<250;根据如果每人交9元,还用不了可得9x>250.
试题解析:设参加春游的同学x人,由题意得
.
见解析
【解析】试题分析:根据每人交8元钱租车费,还不够可得8x<250;根据如果每人交9元,还用不了可得9x>250.
试题解析:设参加春游的同学x人,由题意得
.
练习册系列答案
相关题目
不改变分式的值,使下列分式的分子和分母的最高次项的系数为正数.
(1)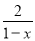 ; (2)
; (2)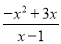 ; (3)
; (3)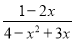 .
.
 (1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) =
(1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) = 若n边形内角和为900°,则边数n= .
 7.
【解析】
试题分析:根据题意得:180(n﹣2)=900,解得:n=7.故答案为:7.
7.
【解析】
试题分析:根据题意得:180(n﹣2)=900,解得:n=7.故答案为:7. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是__.
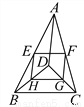
 11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11. 如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE= .
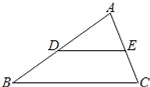
 4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4.
4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4. 有如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,从图形上确定这两个广告牌面积的大小关系,并将这种大小关系用含字母a,b的不等式表示为__________.

 a2+b2>ab (a≠b)
【解析】试题分析:由图上可看出:图1可看做是长为a,宽为b的长方形加上一个小直角三角形;图2可看做是长为a,宽为b的长方形,根据不等关系:图1的面积>图2的面积,即可列出不等式.
根据图形的面积公式,得图1的面积是a2+b2,图2的面积是ab
再根据图形的面积大小关系,得a2+b2>ab(a≠b).
a2+b2>ab (a≠b)
【解析】试题分析:由图上可看出:图1可看做是长为a,宽为b的长方形加上一个小直角三角形;图2可看做是长为a,宽为b的长方形,根据不等关系:图1的面积>图2的面积,即可列出不等式.
根据图形的面积公式,得图1的面积是a2+b2,图2的面积是ab
再根据图形的面积大小关系,得a2+b2>ab(a≠b). 小林在水果摊上称了2斤苹果,摊主称了几个苹果说:“你看秤,高高的.”如果设苹果的实际质量为x斤,用不等式把这个“高高的”的意思表示出来是( )
A.x≤2 B.x≥2 C.x>2 D.x<2
 C
【解析】
试题分析:理【解析】
高高的意思说比本身质量高.
【解析】
由题意:x>2.
故选C.
C
【解析】
试题分析:理【解析】
高高的意思说比本身质量高.
【解析】
由题意:x>2.
故选C. 如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点,下列结论中错误的是( )
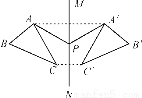
A. △AA′P是等腰三角形 B. MN垂直平分AA′,CC′
C. △ABC与△A′B′C′面积相等 D. 直线AB、A′B′的交点不一定在MN上
 D
【解析】试题分析:△ABC与△A′B′C′关于直线MN对称,P为MN上任一点,所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分,所以△AA′P是等腰三角形;MN垂直平分AA′,CC′;△ABC与△A′B′C′面积相等;AA′
D
【解析】试题分析:△ABC与△A′B′C′关于直线MN对称,P为MN上任一点,所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分,所以△AA′P是等腰三角形;MN垂直平分AA′,CC′;△ABC与△A′B′C′面积相等;AA′如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为点F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
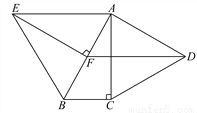
 (1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=...
(1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=... 
