��Ŀ����
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=8��AB="10." DE��ֱƽ��AC��AB�ڵ�E����DE�ij�Ϊ�� ��
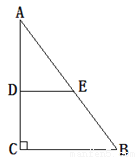
A. 6 B. 5 C. 4 D. 3
 D
�������������������֪���ڡ�ABC�У���ACB=90�㣬AC=8��AB=10�����ݹ��ɶ����ɵ�BC=6������DE��ֱƽ��AC����ACB=90�㣬�ɵ�DEΪ��ABC����λ�ߣ����������ε���λ�߶����ɵ�DE=BC=3���ʴ�ѡD.
D
�������������������֪���ڡ�ABC�У���ACB=90�㣬AC=8��AB=10�����ݹ��ɶ����ɵ�BC=6������DE��ֱƽ��AC����ACB=90�㣬�ɵ�DEΪ��ABC����λ�ߣ����������ε���λ�߶����ɵ�DE=BC=3���ʴ�ѡD.
 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д���ͼ���ڡ�ABD�У�AC��BD����C��BD���е㣬�����н��۴�����ǣ� ��
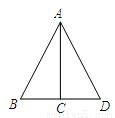
A. AB=AD B. AB=BD C. ��B=��D D. ACƽ�֡�BAD
 B
����������AC��BD����C��BD���е㣬
��AB=AD���߶��д��ߵ����ʣ�
���B=��D���ȱ߶ԵȽǣ�
���BAC=��DAC���������������ߺ�һ��
��ACƽ�֡�BAD��
��ѡ��B .
B
����������AC��BD����C��BD���е㣬
��AB=AD���߶��д��ߵ����ʣ�
���B=��D���ȱ߶ԵȽǣ�
���BAC=��DAC���������������ߺ�һ��
��ACƽ�֡�BAD��
��ѡ��B . ��ͼ��AC���������ABCDE��һ���Խ��ߣ����ACB= ��
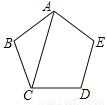
 36�㣮
��������
����������������ABCDE��������Σ����B=108�㣬AB=CB�����ACB=��180�㩁108�㣩��2=36�㣻�ʴ�Ϊ��36�㣮
36�㣮
��������
����������������ABCDE��������Σ����B=108�㣬AB=CB�����ACB=��180�㩁108�㣩��2=36�㣻�ʴ�Ϊ��36�㣮 ��ABC�У�D��E�ֱ�ΪAB��AC���е㣬��DE��4��AD��3��AE��2�����ABC���ܳ�Ϊ______��
 18
���������ߵ�D��E�ֱ��ǡ�ABC�ı�AB��AC���е㣬
��DE�ǡ�ABC����λ�ߣ�
��AB=2AD=2��3=6��AC=2AE��2��2=4��BC=2DE=2��4=8��
��AB+AC+BC=18��
����ABC���ܳ�Ϊ18��
�ʴ�Ϊ��18.
18
���������ߵ�D��E�ֱ��ǡ�ABC�ı�AB��AC���е㣬
��DE�ǡ�ABC����λ�ߣ�
��AB=2AD=2��3=6��AC=2AE��2��2=4��BC=2DE=2��4=8��
��AB+AC+BC=18��
����ABC���ܳ�Ϊ18��
�ʴ�Ϊ��18. ��ͼ��D�ǡ�ABC��һ�㣬BD��CD��AD��6��BD��4��CD��3��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬���ı���EFGH���ܳ���__.
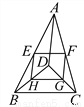
 11
�������������������BD��DC��BD=4��CD=3���ɹ��ɶ����ã�
��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬
��HG=BC=EF��EH=FG=AD��
��AD="6��"
��EF="HG=2.5��EH=GF=3��"
���ı���EFGH���ܳ���EF+FG+HG+EH=2����2.5+3��=11��
11
�������������������BD��DC��BD=4��CD=3���ɹ��ɶ����ã�
��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬
��HG=BC=EF��EH=FG=AD��
��AD="6��"
��EF="HG=2.5��EH=GF=3��"
���ı���EFGH���ܳ���EF+FG+HG+EH=2����2.5+3��=11�� ij����ѧ���飬����16��ѡ���⣬���ַ����ǣ����һ���6�֣��������һ���2�֣�ijͬѧҪ��÷�Ϊ60�����ϣ�������Ӧ��Զ��ٵ���?(ֻ�й�ϵʽ)
 6x��2(16��x)��60
�������������������ϵʽΪ��6����Ե�����-2������������60���ݴ��в���ʽ����.
������������ͬѧӦ���x���⣬�������
6x��2(16��x) ��60.
6x��2(16��x)��60
�������������������ϵʽΪ��6����Ե�����-2������������60���ݴ��в���ʽ����.
������������ͬѧӦ���x���⣬�������
6x��2(16��x) ��60. ����ͼ��ʾ�����ֹ���ƣ�����ͼ��1��������������ֱ�������ι��ɵģ�ͼ��2����һ�����Σ���ͼ����ȷ�����������������Ĵ�С��ϵ���������ִ�С��ϵ�ú���ĸa��b�IJ���ʽ��ʾΪ__________��

 a2��b2��ab (a��b)
�������������������ͼ�Ͽɿ�����ͼ1�ɿ����dz�Ϊa����Ϊb�ij����μ���һ��Сֱ�������Σ�ͼ2�ɿ����dz�Ϊa����Ϊb�ij����Σ����ݲ��ȹ�ϵ��ͼ1�������ͼ2������������г�����ʽ��
����ͼ�ε������ʽ����ͼ1�������a2��b2��ͼ2�������ab
�ٸ���ͼ�ε������С��ϵ����a2��b2��ab��a��b��.
a2��b2��ab (a��b)
�������������������ͼ�Ͽɿ�����ͼ1�ɿ����dz�Ϊa����Ϊb�ij����μ���һ��Сֱ�������Σ�ͼ2�ɿ����dz�Ϊa����Ϊb�ij����Σ����ݲ��ȹ�ϵ��ͼ1�������ͼ2������������г�����ʽ��
����ͼ�ε������ʽ����ͼ1�������a2��b2��ͼ2�������ab
�ٸ���ͼ�ε������С��ϵ����a2��b2��ab��a��b��. ��ͼ��ABC�У�AB=BC����A=36�㣬BDƽ�֡�ABC��AC��D����ͼ�еĵ�����������_____��

 3
������������������������ǵĶ������ɴ�ȷ���ĸ��������ǵ���������
��𣺡��ڡ�ABC�У�AB=BC����A=36�㣬
���ABC=��ACB =72�㣬
��BDƽ�֡�ABC��
���ABD=��CBD =36�㣬
���ABD=��A =36�㣬��BDC =72��=��C��
���ABD�͡�BDC���ǵ���������.
������������������ ��������.
3
������������������������ǵĶ������ɴ�ȷ���ĸ��������ǵ���������
��𣺡��ڡ�ABC�У�AB=BC����A=36�㣬
���ABC=��ACB =72�㣬
��BDƽ�֡�ABC��
���ABD=��CBD =36�㣬
���ABD=��A =36�㣬��BDC =72��=��C��
���ABD�͡�BDC���ǵ���������.
������������������ ��������. �۲�����ƽ��ͼ�Σ�����������Գ�ͼ�ε���( )

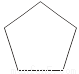
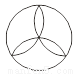

A. 1�� B. 2�� C. 3�� D. 4��
 C
��������������Գ�ͼ�εĶ����֪��ǰ����ͼ�ηֱ���5����5����3���Գ��ᣬ���һ��ͼ���������ڵ�ͼ��û�жԳ���.
��ѡC.
C
��������������Գ�ͼ�εĶ����֪��ǰ����ͼ�ηֱ���5����5����3���Գ��ᣬ���һ��ͼ���������ڵ�ͼ��û�жԳ���.
��ѡC. 
