题目内容
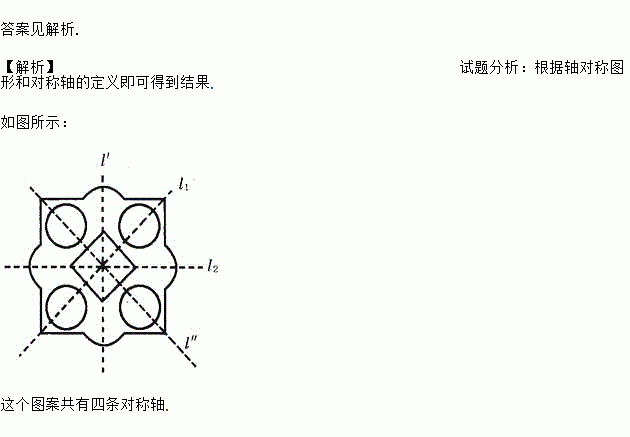
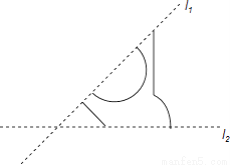
如图，两条相交直线l1与l2的夹角是45°，都是一个图案的对称轴，画出这个图案的其余部分．这个图案共有多少条对称轴？
答案见解析.
【解析】试题分析：根据轴对称图形和对称轴的定义即可得到结果.
如图所示：
这个图案共有四条对称轴.
练习册系列答案
相关题目
在代数式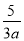
， 
， 
， 
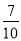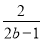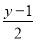，x+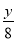
中，是分式的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】在代数式， ，， ，x+的分母中均不含有字母，因此它们是整式，而不是分式．
而,分母中含有字母，因此是分式．
故选B. 如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是__.
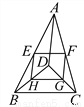
11
【解析】试题解析：∵BD⊥DC，BD=4，CD=3，由勾股定理得，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴HG=BC=EF，EH=FG=AD，
∵AD="6，"
∴EF="HG=2.5，EH=GF=3，"
∴四边形EFGH的周长是EF+FG+HG+EH=2×（2.5+3）=11． 有如图所示的两种广告牌，其中图（1）是由两个等腰直角三角形构成的，图（2）是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a，b的不等式表示为__________．
a2＋b2＞ab (a≠b)
【解析】试题分析：由图上可看出：图1可看做是长为a，宽为b的长方形加上一个小直角三角形；图2可看做是长为a，宽为b的长方形，根据不等关系：图1的面积＞图2的面积，即可列出不等式．
根据图形的面积公式，得图1的面积是a2＋b2，图2的面积是ab
再根据图形的面积大小关系，得a2＋b2＞ab（a≠b）. 小林在水果摊上称了2斤苹果，摊主称了几个苹果说：“你看秤，高高的．”如果设苹果的实际质量为x斤，用不等式把这个“高高的”的意思表示出来是（ ）
A.x≤2 B.x≥2 C.x＞2 D.x＜2
C
【解析】
试题分析：理【解析】
高高的意思说比本身质量高．
【解析】
由题意：x＞2．
故选C． 如图△ABC中，AB=BC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有_____个
3
【解析】根据条件求出各个角的度数，由此确定哪个三角形是等腰三角形
解答：∵在△ABC中，AB=BC，∠A=36°，
∴∠ABC=∠ACB =72°，
∵BD平分∠ABC，
∴∠ABD=∠CBD =36°，
∴∠ABD=∠A =36°，∠BDC =72°=∠C，
∴△ABD和△BDC都是等腰三角形.
故有三个等腰三角形 故有三个. 如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，下列结论中错误的是（ ）
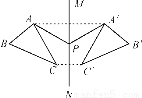
A. △AA′P是等腰三角形 B. MN垂直平分AA′，CC′
C. △ABC与△A′B′C′面积相等 D. 直线AB、A′B′的交点不一定在MN上
D
【解析】试题分析：△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分，所以△AA′P是等腰三角形；MN垂直平分AA′，CC′；△ABC与△A′B′C′面积相等；AA′找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.
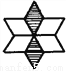
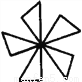
（1） (2) (3)
见解析
【解析】试题分析：本题考查了利用轴对称设计图案的知识,解答本题的关键是熟练掌握轴对称的性质.观察可知①是轴对称图形,先确定对称轴,然后找对应点、对应线段及对应角.
【解析】
第一个图形是轴对称图形，第二、三个图形是旋转对称图形.
如上图所示，若以EF为对称轴,则点A与点B、点M与点N、点C与点D等是对应点.线段AG与BH、CM与DN、PG与PH等是对应线段,∠A与∠B、... 下列给出的是四边形ABCD中∠A、∠B、∠C、∠D的度数之比，其中能说明四边形ABCD为平行四边形的是（ ）
A. 1：2：3：4 B. 2：2：3：4 C. 2：3：2：3 D. 2：3：3：2
C
【解析】【解析】
由平行四边形的两组对角分别相等，可知C正确．故选C．