题目内容
2.已知⊙O中,弦AB⊥AC,且AB=AC=6,点D在⊙O上,连接AD,BD,CD.(1)如图1,若AD经过圆心O,求BD,CD的长;
(2)如图2,若∠BAD=2∠DAC,求BD,CD的长.
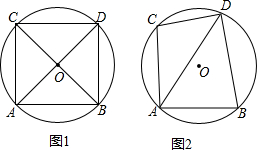
分析 (1)由AD经过圆心O,利用圆周角定理得∠ACD=∠ABD=90°,又因为AB⊥AC,且AB=AC=6,易得四边形ABCD为正方形,易得结果;
(2)连接OC,OB,OD,由∠BAD=2∠DAC,AB⊥AC,由圆周角定理得BC为直径,易得∠CAD=30°,∠BAD=60°,BO=CO=DO=$\frac{1}{2}$BC=3$\sqrt{2}$,由圆周角定理得∠COD=60°,∠BOD=120°,△COD为等边三角形,求得CD,BD.
解答 解:(1)∵AD经过圆心O,
∴∠ACD=∠ABD=90°,
∵AB⊥AC,且AB=AC=6,
∴四边形ABCD为正方形,
∴BD=CD=AB=AC=6;
(2)连接OC,OB,OD,过O点作OE⊥BD,
∵AB⊥AC,AB=AC=6,
∴BC为直径,
∴BC=6$\sqrt{2}$,
∴BO=CO=DO=$\frac{1}{2}$BC=3$\sqrt{2}$,
∵∠BAD=2∠DAC,
∴∠CAD=30°,∠BAD=60°,
∴∠COD=60°,∠BOD=120,
∴△COD为等边三角形,∠BOE=60°,
∴CD=CO=DO=3$\sqrt{2}$,
在直角三角形CDB中,BD=$\sqrt{3}$CD=3$\sqrt{6}$,
则BE=$\frac{3\sqrt{6}}{2}$,
∵OE⊥BD,
∴BD=2BE=3$\sqrt{6}$.
点评 本题主要考查了圆周角定理,垂径定理,数形结合,作出适当的辅助线是解答此题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.下列各式不是一元一次不等式组的是( )
| A. | $\left\{\begin{array}{l}{x>3}\\{x<1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x<5}\\{2x-1<9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-1>3}\\{y+2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1>3}\\{x-3<2}\\{2x-1<5}\end{array}\right.$ |
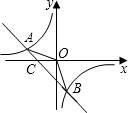 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点. 如图,在?ABCD中,AE,BF,CM,DN分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线.求证:四边形GHKL是矩形.
如图,在?ABCD中,AE,BF,CM,DN分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线.求证:四边形GHKL是矩形. 在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm.
在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm.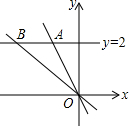 如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.
如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.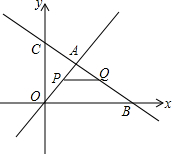 如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.|
如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.|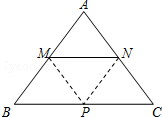 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.