题目内容
10. 如图,在?ABCD中,AE,BF,CM,DN分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线.求证:四边形GHKL是矩形.
如图,在?ABCD中,AE,BF,CM,DN分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线.求证:四边形GHKL是矩形.
分析 首先根据平行四边形的性质可得∠DAB+∠ABC=180°,再根据角平分线的性质可得∠GAB+∠GBA=$\frac{1}{2}$(∠DAB+∠ABC)=$\frac{1}{2}$×180°=90°,然后同理可得:∠GLK=90°,∠LKH=90°,∠KHG=90°,根据三个角是直角的四边形是矩形可得四边形GHKL是矩形.
解答 解:四边形GHKL是矩形,
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE,BF分别平分∠DAB,∠ABC,
∴∠GAB+∠GBA=$\frac{1}{2}$(∠DAB+∠ABC)=$\frac{1}{2}$×180°=90°.
∴∠LGH=90°,
同理:∠GLK=90°,∠LKH=90°,
∴∠KHG=90°,
∴四边形GHKL是矩形.
点评 此题主要考查了矩形的判定,平行四边形的性质,关键是掌握三个角是直角的四边形是矩形.

练习册系列答案
相关题目
1.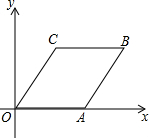 如图,四边形OABC是边长为4的菱形,且∠B=60°.
如图,四边形OABC是边长为4的菱形,且∠B=60°.
(1)求点B与点C的坐标;
(2)若将四边形OABC绕点O按顺时针方向旋转60°,点B恰好落在双曲线y=$\frac{k}{x}$上,求k的值.
 如图,四边形OABC是边长为4的菱形,且∠B=60°.
如图,四边形OABC是边长为4的菱形,且∠B=60°.(1)求点B与点C的坐标;
(2)若将四边形OABC绕点O按顺时针方向旋转60°,点B恰好落在双曲线y=$\frac{k}{x}$上,求k的值.
5.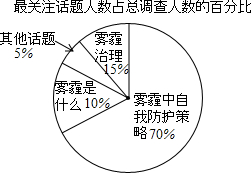 2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
(1)参加本次街头随访和网络调查的总人数是2000人,a的值为300;
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是$\frac{10}{13}$;
(4)通过这次调查,你有什么想法?
 2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格. | 最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
| 雾霾是什么 | 80 | 120 | 200 |
| 雾霾治理 | 40%a | 60%a | a |
| 雾霾中自我防护策略 | 800 | 600 | 1400 |
| 其他话题 | 40 | 60 | 100 |
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是$\frac{10}{13}$;
(4)通过这次调查,你有什么想法?
 如图,点D、E、F分别在等边三角形ABC的边AB、BC、CA的延长线上,且BD=CE=AF,说明△DEF为等边三角形.
如图,点D、E、F分别在等边三角形ABC的边AB、BC、CA的延长线上,且BD=CE=AF,说明△DEF为等边三角形.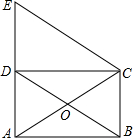 如图,矩形ABCD的对角线AC、BD相交于点O,过点C作BD的平行线与AD的延长线相交于点E.求证:△ACE是等腰三角形.
如图,矩形ABCD的对角线AC、BD相交于点O,过点C作BD的平行线与AD的延长线相交于点E.求证:△ACE是等腰三角形.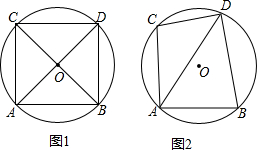
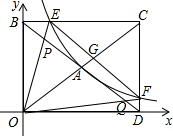 如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.
如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.