题目内容
13.某商场经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)的相关信息如下:| 售价x(元) | 60 | 70 | 80 | 90 | … |
| 销售量y(件) | 280 | 260 | 240 | 220 | … |
(2)售价为多少元时,当月的利润最大?最大利润是多少?
分析 (1)由x的值每增加10元时,y的值均减小20件知这个函数为一次函数,待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,再配方成顶点式依据二次函数的性质是解题的关键.
解答 解:(1)由表可知,x的值每增加10元时,y的值均减小20件,
据此可知y与x的函数关系为一次函数,
设该一次函数为y=k x+b,
代入(60,280)和(70,260),
得:$\left\{\begin{array}{l}{60k+b=280}\\{70k+b=260}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=400}\end{array}\right.$,
∴y=-2x+400,
将(80,240),(90,220)代入上式等式成立;
故答案为:一次函数.
(2)设月利润为w元,
则w=(x-40)y=(x-40)(-2x+400)=-2(x-120)2+12800,
∵-2<0,
∴当x=120时,w有最大值12800,
答:当售价定为120元时,利润最大,最大值为12800元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及根据相等关系列出函数解析式是解题的关键.

练习册系列答案
相关题目
18.某超市在50天内试销一款成本40元/件的新型商品,了解到此款商品第x天的销售信息如下表:
(1)当第5或45天时,该商品的销售单价为65元/件;
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
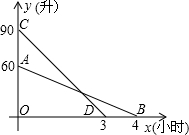 “滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.
“滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.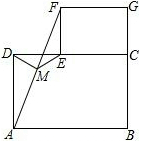 猜想与证明:
猜想与证明: 如图,矩形ABCD的对角线AC、BD相交于点O,OA=3,则BD的长为6.
如图,矩形ABCD的对角线AC、BD相交于点O,OA=3,则BD的长为6.