题目内容
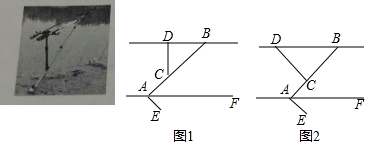
3.如图1是一种折叠式可凋节钓鱼竿支架的示意图,AE是地插,用来将支架固定在地面上,支架AB可绕A点前后转动,用来调节AB与地面的夹角,支架CD可绕支点C前后转动,用来调节CD与AB的夹角,支架CD带有伸缩调节长度的功能.(1)若支架CD与地面垂直,钓鱼竿DB与地面AF平行,AC=30cm,BC=60cm,CD=40cm,则钓鱼竿BD距地面的高度为60cm;
(2)如图2,保持(1)中支架AB与地面的夹角不变,凋节支架CD与AB的夹角,使得∠DCB=90°,若要使钓鱼竿DB与地面AF仍然保持平行,则支架CD的长度应该调节为多少?(结果保留根号)
分析 (1)由平行得:∠DBC=∠CAG,根据等角的三角函数列式,求CG的长,距离为DG可求;
(2)由(1)的结论,根据∠HCB=∠CDB,cos∠HCB=cos∠CDB=$\frac{CH}{BC}=\frac{DH}{DC}$,设DH=2x,DC=3x,
由勾股定理列方程可得结论.
解答 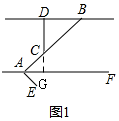 解:(1)如图1,延长DC交AF于G,
解:(1)如图1,延长DC交AF于G,
∵CD⊥BD,BD∥AF,
∴CD⊥AF,∠DBC=∠CAG,
sin∠DBC=sin∠CAG=$\frac{CD}{BC}=\frac{CG}{AC}$,
∴$\frac{40}{60}=\frac{CG}{30}$,
∴CG=20,
∴DG=40+20=60,
即钓鱼竿BD距地面的高度为60cm;
故答案为:60;
(2)如图2,过C作GH⊥BD,交BD于H,交AF于G,则GH⊥AF,
由(1)得:CH=40,BC=60,
∵∠BCD=90°,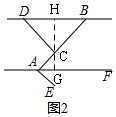
∴∠CDB+∠DBC=90°,
∵∠HCB+∠DBC=90°,
∴∠HCB=∠CDB,
cos∠HCB=cos∠CDB=$\frac{CH}{BC}=\frac{DH}{DC}$,
∴$\frac{40}{60}=\frac{DH}{DC}=\frac{2}{3}$,
设DH=2x,DC=3x,
由勾股定理得:(2x)2+402=(3x)2,
x=$±8\sqrt{5}$,
∵x>0,
∴x=8$\sqrt{5}$,
∴CD=3x=24$\sqrt{5}$,
答:支架CD的长度应该调节为24$\sqrt{5}$cm.
点评 本题是解直角三角形的应用问题,考查了三角函数、勾股定理、平行线的性质,熟练掌握三角函数的定义是关键.

练习册系列答案
相关题目
1.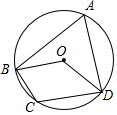 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
8.现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
(1)根据题意,填写下表:
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
(3)小明应选择哪家快递公司更省钱?
13.某商场经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)的相关信息如下:
(1)试用你学过的函数来描述y与x的关系,这个函数可以是一次函数(填一次函数、反比例函数或二次函数),求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
| 售价x(元) | 60 | 70 | 80 | 90 | … |
| 销售量y(件) | 280 | 260 | 240 | 220 | … |
(2)售价为多少元时,当月的利润最大?最大利润是多少?
 如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度.
如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度.