题目内容
 如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P.则DP的长为
如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P.则DP的长为考点:旋转的性质,二次函数图象上点的坐标特征
专题:
分析:先把A点坐标代入y=ax2求出a=1,得到抛物线的解析式为y=x2,再根据旋转的性质得OD=OB=2,∠ODC=∠OBA=90°,所以D点坐标为(0,2),CD⊥y轴,即P点的纵坐标为2,然后把y=2代入抛物线解析式计算出对应的自变量的值,于是确定P点坐标,利用P点坐标易得PD的长.
解答: 解:把A(-2,4)代入y=ax2得4a=4,解得a=1,
解:把A(-2,4)代入y=ax2得4a=4,解得a=1,
∴抛物线的解析式为y=x2,
∵Rt△OAB的顶点A的坐标为(-2,4),AB⊥x轴,
∴AB=4,OB=2,
∵Rt△OAB绕点O顺时针旋转90°得到△OCD,
∴OD=OB=2,∠ODC=∠OBA=90°,
∴D点坐标为(0,2),CD⊥y轴,
∴P点的纵坐标为2,
把y=2代入y=x2得x2=2,解得x=±
(负值舍去),
∴P点坐标为(
,2),
∴PD=
.
故答案为:
.
 解:把A(-2,4)代入y=ax2得4a=4,解得a=1,
解:把A(-2,4)代入y=ax2得4a=4,解得a=1,∴抛物线的解析式为y=x2,
∵Rt△OAB的顶点A的坐标为(-2,4),AB⊥x轴,
∴AB=4,OB=2,
∵Rt△OAB绕点O顺时针旋转90°得到△OCD,
∴OD=OB=2,∠ODC=∠OBA=90°,
∴D点坐标为(0,2),CD⊥y轴,
∴P点的纵坐标为2,
把y=2代入y=x2得x2=2,解得x=±
| 2 |
∴P点坐标为(
| 2 |
∴PD=
| 2 |
故答案为:
| 2 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了二次函数图象上点的坐标特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
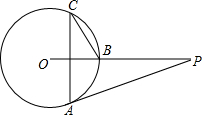 如图,P是⊙O外一点,PA是⊙O的切线,A为切点,PO与⊙O相交于 B点,已知∠P=28°,C为⊙O上一点,连接CA,CB,则∠C的度数为( )
如图,P是⊙O外一点,PA是⊙O的切线,A为切点,PO与⊙O相交于 B点,已知∠P=28°,C为⊙O上一点,连接CA,CB,则∠C的度数为( )| A、28° | B、62° |
| C、31° | D、56° |
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上). 在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标分别为A(
在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标分别为A(