抛物线y=x2-2的顶点坐标为( )A．B．C．(0.2)D．(2.0) 题目和参考答案——青夏教育精英家教网——

题目内容

12．抛物线y=x²-2的顶点坐标为（　　）

A．

（0，-2）

B．

（-2，0）

C．

（0，2）

D．

（2，0）

分析根据顶点式的坐标特点，直接写出顶点坐标即对称轴．

解答解：抛物线y=x²-2是顶点式，
根据顶点式的坐标特点可知，
顶点坐标为（0，-2），
故选A．

点评此题考查了二次函数的性质，二次函数y=a（x-h）²+k的顶点坐标为（h，k），对称轴为x=h．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

2．已知二次函数y=ax²+bx+c（a＞0）经过点M（-1，2）和点N（1，-2），交x轴于A，B两点，交y轴于C．则：①b=-2； ②该二次函数图象与y轴交于负半轴； ③存在这样一个a，使得M、A、C三点在同一条直线上； ④若a=1，则OA•OB=OC²．以上说法正确的有（　　）

如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A₁，B₁，C₁，使A₁B=AB，B₁C=BC，C₁A=CA，顺次连接A₁，B₁，C₁，得到△A₁B₁C₁．第二次操作：分别延长A₁B₁，B₁C₁，C₁A₁至点A₂，B₂，C₂，使A₂B₁=A₁B₁，B₂C₁=B₁C₁，C₂A₁=C₁A₁，顺次连接A₂，B₂，C₂，得到△A₂B₂C₂，…按此规律，要使得到的三角形的面积超过2016，最少经过（　　）次操作．

我们可以计算出
①$\sqrt{{2}^{2}}$=2　$\sqrt{（\frac{2}{3}）^{2}}$=$\frac{2}{3}$；$\sqrt{{3}^{2}}$=3
而且还可以计算$\sqrt{（-2）^{2}}$=2$\sqrt{（-{\frac{2}{3}）}^{2}}$=$\frac{2}{3}$$\sqrt{（-3）^{2}}$=3
（1）根据计算的结果，可以得到：①当a＞0时$\sqrt{{a}^{2}}$=a；②当a＜0时$\sqrt{{a}^{2}}$=-a．
（2）应用所得的结论解决：如图，已知a，b在数轴上的位置，化简$\sqrt{a^2}$-$\sqrt{b^2}$-$\sqrt{{{（a+b）}^2}}$．

7．计算：[（-3x²y⁴）²•x³-2x•（3x²y²）³$•\frac{1}{3}$y²]÷9x⁷y⁸．

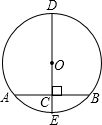如图，DE是⊙O的直径，弦AB⊥DE，垂足为C，若AB=8，OC=3．求⊙O的半径．

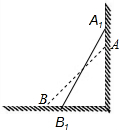如图所示，一架5米长的消防梯子斜靠在一竖直的墙AC上，梯足（点B）离墙底端（C点）的距离为3米，如果梯足内移1.6米至点B处，则梯子顶端沿墙垂直上移0.8米．

1．若|a-b|+$\sqrt{b-1}$=0，则a=1．

2．下列语句是命题的是（　　）

	A．	相等的角是对顶角		B．	同位角相等，两直线平行吗？
	C．	作∠AOB的平分线OC		D．	延长线AB到C使AC=2AB