题目内容
15.有一块直角三角形纸片,两直角边AC=6cm,BC=8cm.①如图1,现将纸片沿直线AD折叠,使直角边AC落在斜边AB上,则CD=3 cm.
②如图2,若将直角∠C沿MN折叠,点C与AB中点H重合,点M、N分别在AC、BC上,则AM2、BN2与MN2之间有怎样的数量关系?并证明你的结论.
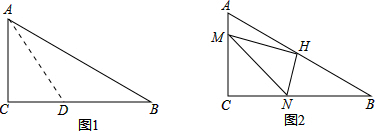
分析 (1)先求得AB的长,然后由翻折的性质可知DC′⊥AB,DC′=DC,最后根据SACD+SADB=S△ABC即可求得CD的长;
(2)过点B作BP∥AC交MH延长线于点P,连接NP,首先证明△AMH≌△BPH,AM=BP,MH=PH,由线段垂直平分线的性质得到MN=NP,在Rt△NBP中利用勾股定理证明即可.
解答 解:(1)如图1所示.
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}=10$.
由翻折的性质可知:DC′⊥AB,DC′=DC.
∵SACD+SADB=S△ABC,
∴$\frac{1}{2}AC•CD+\frac{1}{2}AB•C′D=\frac{1}{2}AC•CB$.
∴$\frac{1}{2}×6×CD+\frac{1}{2}×10×C′D=\frac{1}{2}×6×8$.
又∵CD=C′D,
∴3CD+5CD=24.
∴CD=3.
(2)AM2+BN2=MN2.
证明:过点B作BP∥AC交MH延长线于点P,连接NP.
∵BP∥AC,
∴∠A=∠PBH
在△AMH和△BPH中,
$\left\{\begin{array}{l}{∠A=∠PBH}\\{AH=BH}\\{∠AHM=∠BHP}\end{array}\right.$,
∴△AMH≌△BPH.
∴AM=BP,MH=PH.
又∵NH⊥MP
∴MN=NP
∵BP∥AC,∠C=90°
∴∠NBP=90°
∴BP2+BN2=NP2
∴AM2+BN2=MN2.
点评 本题主要考查的是翻折的性质、勾股定理、全等三角形的判定和性质,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
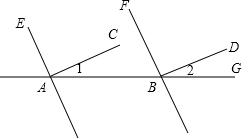 如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF.
如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF. 如图,△ABC中,M是BC中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
如图,△ABC中,M是BC中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.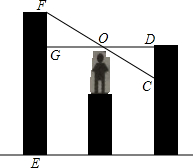 如图,某建筑公司想测出一电视塔EF的高度,身高为1.71m的公司员工登上10m高的顶楼阳台,他固定自己的站立位置,看到该电视塔的最高点时测出视线的仰角,再转过一个角度,用同样的大小的角度作为俯角,使视线刚好落在该员工的距离等于他与电视塔的距离的另一个建筑物的某一点C上,然后测出与该员工在同一水平线上的另一建筑物上的点D到点C的距离CD,就可以利用该距离求出该电视塔的高度,你能将其表示出来吗?
如图,某建筑公司想测出一电视塔EF的高度,身高为1.71m的公司员工登上10m高的顶楼阳台,他固定自己的站立位置,看到该电视塔的最高点时测出视线的仰角,再转过一个角度,用同样的大小的角度作为俯角,使视线刚好落在该员工的距离等于他与电视塔的距离的另一个建筑物的某一点C上,然后测出与该员工在同一水平线上的另一建筑物上的点D到点C的距离CD,就可以利用该距离求出该电视塔的高度,你能将其表示出来吗? 如图,A、B、C是一条直线上的三个点,A、B间的距离为100cm,A、C间的距离为40cm,现在A、B之间有一动点P,设P、C之间的距离为xcm
如图,A、B、C是一条直线上的三个点,A、B间的距离为100cm,A、C间的距离为40cm,现在A、B之间有一动点P,设P、C之间的距离为xcm