题目内容
3.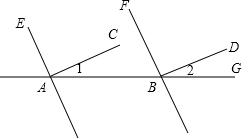 如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF.
如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF.
分析 已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,故可按同位角相等两直线平行判断AC∥BD、AE∥BF.
解答 解:∵∠1=∠2=35°,
∴AC∥BD;
∵AC⊥AE,BD⊥BF,
∴∠EAC=∠FBD,
∵∠1=∠2,
∴∠EAB=∠EAC+∠1,∠FBG=∠FBD+∠2,
∴∠EAB=∠FBG,
∴AE∥BF.
点评 本题考查了平行线的判定与性质,可围绕截线找同位角、内错角和同旁内角.只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11.满足下列条件的△ABC中,不是直角三角形的是( )
| A. | ∠B+∠A=∠C | B. | ∠A:∠B:∠C=2:3:5 | ||
| C. | ∠A=2∠B=3∠C | D. | 一个外角等于和它相邻的一个内角 |
8.在△ABC中,若∠A:∠B:∠C=4:3:1,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
12.下列说法中,错误的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线平分对角的平行四边形是菱形 | |
| C. | 四个内角相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
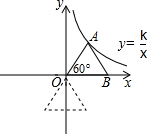 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.