题目内容
5.化简:$\frac{n}{m}\sqrt{\frac{n}{2{m}^{3}}}$•(-$\frac{1}{m}\sqrt{\frac{{n}^{3}}{{m}^{3}}}$) $÷\sqrt{\frac{n}{2{m}^{3}}}$(m>0,n>0)分析 根据二次根式的乘除法,即可解答,注意结果化到最简.
解答 解:原式=$\frac{n}{{m}^{2}}\sqrt{\frac{n}{2m}}•(-\frac{n}{{m}^{2}}\sqrt{\frac{n}{m}})•m\sqrt{\frac{2m}{n}}$
=-$\frac{{n}^{2}}{{m}^{3}}\sqrt{\frac{n}{m}}$
=-$\frac{{n}^{2}}{{m}^{4}}\sqrt{mn}$.
点评 本题考查了二次根式的乘除法,解决本题的关键是在计算过程中注意化简.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
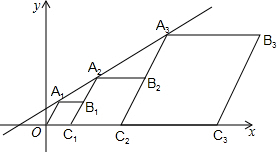 菱形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按照如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上.已知∠A1OC1=60°,点B1(3,$\sqrt{3}$),B2(8,2$\sqrt{3}$),则An的坐标是(3•2n-1-2,2n-1•$\sqrt{3}$)(用含n的式子表示)
菱形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按照如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上.已知∠A1OC1=60°,点B1(3,$\sqrt{3}$),B2(8,2$\sqrt{3}$),则An的坐标是(3•2n-1-2,2n-1•$\sqrt{3}$)(用含n的式子表示)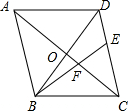 如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.
如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.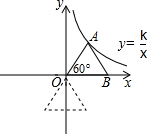 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.