题目内容
4.已知抛物线y=ax2+bx+c(a≠0)经过点B(2,0)和点C(0,8),且它的对称轴是直线x=-2.(1)求抛物线与x轴的另一交点A的坐标;
(2)求此抛物线的解析式.
分析 (1)根据抛物线的轴对称性即可求出抛物线与x轴的另一交点A的坐标.
(2)根据两点坐标和对称轴就能求出抛物线的解析式.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-2,点B(2,0),
∴由对称性可得A点的坐标为(-6,0);
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,
将A(-6,0)、B(2,0)代入表达式得
$\left\{\begin{array}{l}{36a-6b+8=0}\\{4a+2b+8=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=-\frac{8}{3}}\end{array}\right.$,
∴所求解析式为y=-$\frac{2}{3}$x2-$\frac{8}{3}$x+8.
点评 本题主要考查了抛物线的轴对称性和待定系数法求抛物线解析式,熟悉抛物线的轴对称性和抛物线解析式的求法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中,错误的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线平分对角的平行四边形是菱形 | |
| C. | 四个内角相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
9.-$\frac{1}{2}$的倒数,相反数分别是( )
| A. | 2,2 | B. | -2,$\frac{1}{2}$ | C. | $\frac{1}{2}$,$\frac{1}{2}$ | D. | -$\frac{1}{2}$,-2 |
16.把二次函数y=-2x2+1的图象向左平移1个单位,再向上平移5个单位,所得的二次函数的表达式是 ( )
| A. | y=-2(x-1)2+6 | B. | y=-2(x-1)2-6 | C. | y=-2(x+1)2+6 | D. | y=-2(x+1)2-6 |
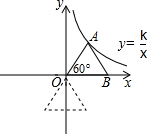 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.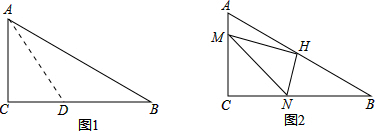
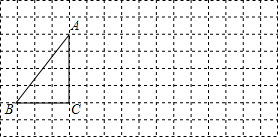 将下列方格纸中的△ABC向右平移8格,得到△A1B1C1.
将下列方格纸中的△ABC向右平移8格,得到△A1B1C1.



 如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.
如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.