题目内容
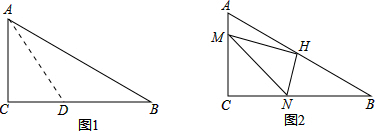
20. 如图,△ABC中,M是BC中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
如图,△ABC中,M是BC中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
分析 延长BD交AC于N,根据等腰三角形三线合一得到BD=DN,AM=AB,根据三角形中位线定理得到DM=$\frac{1}{2}$NC,代入计算即可.
解答  解:延长BD交AC于N,
解:延长BD交AC于N,
∵AD是∠BAC的平分线,BD⊥AD,
∴BD=DN,AN=AB=12,
∵BM=CM,BD=DN,
∴DM=$\frac{1}{2}$NC=$\frac{1}{2}$(AC-AN)=3,
则MD的长为3.
点评 本题考查的是三角形中位线定理和等腰三角形的性质的应用,掌握三角形的中位线平行于第三边且等于第三边的一半和等腰三角形三线合一是解题的关键.

练习册系列答案
相关题目
11.满足下列条件的△ABC中,不是直角三角形的是( )
| A. | ∠B+∠A=∠C | B. | ∠A:∠B:∠C=2:3:5 | ||
| C. | ∠A=2∠B=3∠C | D. | 一个外角等于和它相邻的一个内角 |
8.在△ABC中,若∠A:∠B:∠C=4:3:1,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
5.菱形的面积为32cm2,一个内角是30°,则这个菱形的周长为( )
| A. | 24cm | B. | 28cm | C. | 30cm | D. | 32cm |
12.下列说法中,错误的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线平分对角的平行四边形是菱形 | |
| C. | 四个内角相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
9.-$\frac{1}{2}$的倒数,相反数分别是( )
| A. | 2,2 | B. | -2,$\frac{1}{2}$ | C. | $\frac{1}{2}$,$\frac{1}{2}$ | D. | -$\frac{1}{2}$,-2 |
10.下列交换加数的位置的变形中,正确的是( )
| A. | 1-2+3-4=1+3-2+4 | B. | 1-2+3-4=1-3-2+4 | C. | 1-2+3-4=1+3-2-4 | D. | 1-2+3-4=1-3+2-4 |
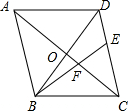 如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.
如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.