题目内容
（1）已知：x=
，y=-1，求x2+2y2-xy的值．
（2）解方程：
+
=1．
| 3 |
（2）解方程：
| 2 |
| x+2 |
| 2 |
| x-1 |
考点：二次根式的化简求值,解分式方程
专题：
分析：（1）直接代入求得数值即可；
（2）按照解分式方程的步骤计算即可．
（2）按照解分式方程的步骤计算即可．
解答：（1）解：当x=
，y=-1，时，
x2+2y2-xy=（
）2+2×（-1）2-
×（-1）
=5+
．
（2）
+
=1
解：去分母，得 2（x-1）+2（x+2）=（x+2）（x-1）
2x-2+2x+4=x2+x-2
x2-3x-4=0
（x-4）（x+1）=0
x1=4，x2=-1
经检验：x1=4，x2=-1都是原方程的根．
∴原方程的根是x1=4，x2=-1．
| 3 |
x2+2y2-xy=（
| 3 |
| 3 |
=5+
| 3 |
（2）
| 2 |
| x+2 |
| 2 |
| x-1 |
解：去分母，得 2（x-1）+2（x+2）=（x+2）（x-1）
2x-2+2x+4=x2+x-2
x2-3x-4=0
（x-4）（x+1）=0
x1=4，x2=-1
经检验：x1=4，x2=-1都是原方程的根．
∴原方程的根是x1=4，x2=-1．
点评：此题考查代数之求值，二次根式的化简，以及解分式方程的步骤与方法．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
已知
m2-2m=6，那么
m2-3m+5的值为（ ）
| 3 |
3
| ||
| 2 |
| A、11 | B、12 | C、13 | D、14 |
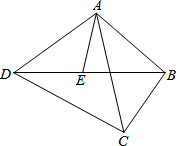已知：如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．
如图，已知在△ABC中，AB=AC，BC=8，tan∠ABC=3，AD⊥BC于D，O是AD上一点，OD=3，以OB为半径的⊙O分别交AB、AC于E、F．求：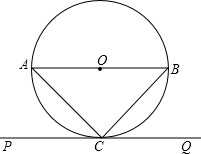
如图，线段AB是圆O的直径，直线PQ经过圆上一点C，PQ∥AB，连结AC、BC，且AC=BC，AC=5
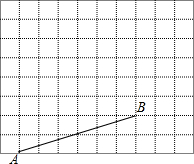如图所示是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，使以A、B、C为顶点的三角形分别满足以下要求：
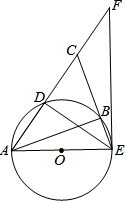如图，AE是⊙O直径，D是⊙O上一点，连结AD并延长使AD=DC，连结CE交⊙O于点B，连结AB．过点E的直线与AC的延长线交于点F，且∠F=∠CED．