题目内容
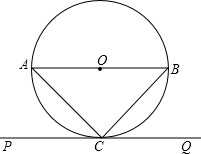 如图,线段AB是圆O的直径,直线PQ经过圆上一点C,PQ∥AB,连结AC、BC,且AC=BC,AC=5
如图,线段AB是圆O的直径,直线PQ经过圆上一点C,PQ∥AB,连结AC、BC,且AC=BC,AC=5| 2 |
(1)求证:PQ是圆O的切线;
(2)求∠CBD的大小.
考点:切线的判定,勾股定理
专题:
分析:(1)利用三角形ABC是等腰直角三角形的性质(三线合一),以及PQ∥AB,得出OC⊥PQ得出结论;
(2)利用勾股定理求得AB的长,进一步分情况探讨:①点D在弧BC上;②点D在弧BA上.
(2)利用勾股定理求得AB的长,进一步分情况探讨:①点D在弧BC上;②点D在弧BA上.
解答:(1)证明:如图,

连接OC,
∵AB是圆O的直径,OA=OB,AC=BC,
∴OC⊥AB
又∵PQ∥AB
∴OC⊥PQ
又∵点C在圆上,PQ经过点C,
∴PQ是圆O的切线.
(2)解:∵AB是圆O的直径,
∴∠ACB=90°,
根据勾股定理,AB=
=10,
点D是圆O上一点,且BD=5
∴OD=OB=BD=5,
∴∠OBD=60°,
又∵AC=BC,
∴∠OBC=45°,
如图,

∴∠CBD=60°+45°=105°,或∠CBD=60°-45°=15°
即∠CBD=105°或15°.

连接OC,
∵AB是圆O的直径,OA=OB,AC=BC,
∴OC⊥AB
又∵PQ∥AB
∴OC⊥PQ
又∵点C在圆上,PQ经过点C,
∴PQ是圆O的切线.
(2)解:∵AB是圆O的直径,
∴∠ACB=90°,
根据勾股定理,AB=
| AC2+BC2 |
点D是圆O上一点,且BD=5
∴OD=OB=BD=5,
∴∠OBD=60°,
又∵AC=BC,
∴∠OBC=45°,
如图,

∴∠CBD=60°+45°=105°,或∠CBD=60°-45°=15°
即∠CBD=105°或15°.
点评:此题考查切线的判定,以及等腰三角形的性质,等边三角形的判定与性质,勾股定理,以及分类讨论思想的渗透.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=30°,则∠α的度数为( )
如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=30°,则∠α的度数为( )| A、25° | B、30° |
| C、20° | D、15° |

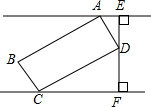 某单位为治理乱停车现象,出台了规范使用停车位的管理办法.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.6m,∠DCF=30°,请你计算车位所占的宽度EF为多少m?(结果保留根号)
某单位为治理乱停车现象,出台了规范使用停车位的管理办法.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.6m,∠DCF=30°,请你计算车位所占的宽度EF为多少m?(结果保留根号) 如图,已知反比例函数y1=
如图,已知反比例函数y1=