题目内容
5.为发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,所使用的便民卡和如意卡在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数关系式.
(2)若每月的通话时间小于30分钟,选择哪种卡合算?
(3)通话时间为多长时,费用一样?
分析 (1)分别利用待定系数法求一次函数解析式和待定系数法求正比例函数解析式求解;
(2)当两种卡的收费相等时,可求出x值,当通话时间小于此值,便民卡便宜,当通话时间大于此值,如意卡便宜.
(3)当两种卡的收费相等时,可求出x值,当通话时间小于此值,便民卡便宜,当通话时间大于此值,如意卡便宜.
解答 解:(1)便民卡:设y1=kx+b,
则$\left\{\begin{array}{l}{b=29}\\{30k+b=35}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=0.2}\\{b=29}\end{array}\right.$,
所以,y1=0.2x+29;
如意卡:设y2=mx,
则30m=15,
解得m=0.5,
所以,y2=0.5x;
把x=2代入y1=0.2x+29=29.4;
把x=2代入y2=0.5x=1;
(2)令y1=y2,即0.2x+29=0.5x,则x=$96\frac{2}{3}$,
当x=$96\frac{2}{3}$,时,y1=y2,两种卡收费一致;
当x<$96\frac{2}{3}$,时,y1>y2,即便民卡便宜;
当x>$96\frac{2}{3}$,时,y1<y2,即如意卡便宜.
每月的通话时间小于30分钟,y1>y2,即便民卡便宜;
(3)当x=$96\frac{2}{3}$,时,y1=y2,两种卡收费一致.
点评 本题考查函数模型的选择及应用,考查了利用待定系数法求一次函数解析式,是基础题.

练习册系列答案
相关题目
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | a-b+c<0 | D. | 4ac-b2<0 |
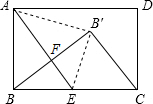 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.