题目内容
18. 如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.
如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.
分析 由A的坐标,以及E为BC中点,确定出OC与CE的长,根据勾股定理求出OE的长,过M作MN⊥OC于N,利用两对角相等的三角形相似得到三角形CMO与三角形ECO相似,由相似得比例求出CM与OM的长,利用面积法求出MN的长,确定出M坐标,求出AM的长,即可得证.
解答 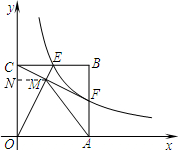 证明:∵OC=4,CE=2,由勾股定理得:OE=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
证明:∵OC=4,CE=2,由勾股定理得:OE=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
过M作MN⊥OC于N,
∵OE⊥CF,
∴∠CMO=∠OCE=90°,
∵∠COE=∠COE,
∴△CMO∽△ECO,
∴$\frac{OC}{OE}$=$\frac{CM}{CE}$=$\frac{OM}{OC}$,
即$\frac{4}{2\sqrt{5}}$=$\frac{CM}{2}$=$\frac{OM}{4}$,
解得:CM=$\frac{4\sqrt{5}}{5}$,OM$\frac{8\sqrt{5}}{5}$,
在△CMO中,由三角形的面积公式得:$\frac{1}{2}$×OC×MN=$\frac{1}{2}$×CM×OM,
即4MN=$\frac{4\sqrt{5}}{5}$×$\frac{8\sqrt{5}}{5}$,
解得:MN=$\frac{8}{5}$,
在△OMN中,由勾股定理得:ON=$\sqrt{O{M}^{2}-M{N}^{2}}$=$\frac{16}{5}$,
即M($\frac{8}{5}$,$\frac{16}{5}$),
∵A(4,0),
∴由勾股定理得:AM=$\sqrt{(4-\frac{8}{5})^{2}+(\frac{16}{5})^{2}}$=4=AO,
则AM=AO.
点评 此题属于反比例函数综合题,涉及的知识有:相似三角形的判定与性质,勾股定理,三角形面积公式,坐标与图形性质,以及反比例函数的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

 如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 25cm |
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=6,则CD的长为2.
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=6,则CD的长为2.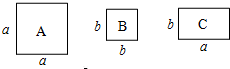 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.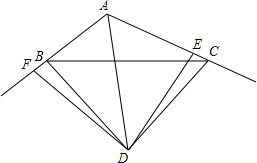 如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论:
如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论: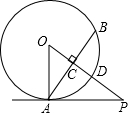 如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长2$\sqrt{3}$.
如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长2$\sqrt{3}$.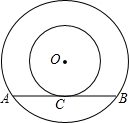 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,求弦AB的长.
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,求弦AB的长.