题目内容
10.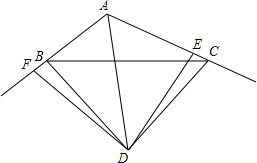 如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论:
如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论:①△CDE≌△BDF
②AB+AC=2AF
③∠BAC+∠BDC=180°
④∠DAC=∠BCD;
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①由角平分线上的点到角两边的距离相等,得出DF=DE,由HL证得Rt△CDE≌Rt△BDF;
②由HL证得Rt△ADE≌Rt△ADF得出AF=AE,由Rt△CDE≌Rt△BDF得出BF=CE,即可得出结果;
③由DE⊥AC,DF⊥AB,得出∠BAC+∠FDE=180°,由Rt△CDE≌Rt△BDF,得出∠FDB=∠EDC,∠FDE=∠BDC,即可得出结果;
④由∠BAC+∠BDC=180°,得出A、B、D、C四点共圆,得出∠BAD=∠BCD,即可得出结果.
解答 解:①∵AD为∠BAC的平分线,DE⊥AC,DF⊥AB,
∴DF=DE,
在Rt△CDE和Rt△BDF中,$\left\{\begin{array}{l}{CD=BD}\\{DE=DF}\end{array}\right.$,
∴Rt△CDE≌Rt△BDF(HL),
∴①正确;
②在Rt△ADE和Rt△ADF中,$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△ADE≌Rt△ADF(HL),
∴AF=AE,
∵Rt△CDE≌Rt△BDF,
∴BF=CE,
∴AB+AC=AB+AE+CE=AB+BF+AE=AF+AE=2AF,
∴②正确;
③∵DE⊥AC,DF⊥AB,
∴∠BAC+∠FDE=180°,
∵Rt△CDE≌Rt△BDF,
∴∠FDB=∠EDC,
∴∠FDE=∠BDC,
∴∠BAC+∠BDC=180°,
∴③正确;
④∵∠BAC+∠BDC=180°,
∴A、B、D、C四点共圆,
∴∠BAD=∠BCD,
∵AD为∠BAC的平分线,
∴∠BAD=∠DAC,
∴∠DAC=∠BCD,
∴④正确;
综上所述:①②③④正确,
故选A.
点评 本题考查了全等三角形的判定与性质、角平分线的性质、四点共圆、同弧所对的圆周角相等等知识;熟练掌握全等三角形的判定与性质和四点共圆是解决问题的关键.

| A. | +5秒 | B. | -5秒 | C. | +10秒 | D. | -10秒 |
| A. | 8 | B. | 12 | C. | -8 | D. | -12 |
| A. | (-a)2•a3=a6 | B. | -a8÷a4=-a2 | C. | $\sqrt{4}$=±2 | D. | (-2a2)3=-8a6 |

 如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体的主视图和左视图.
如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体的主视图和左视图. 如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.
如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.