题目内容
7.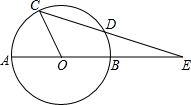 如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=74°,则∠E=($\frac{74}{3}$)°.
如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=74°,则∠E=($\frac{74}{3}$)°.
分析 利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=$\frac{1}{3}$∠AOC进行计算即可.
解答 解:连结OD,如图,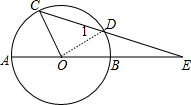
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
∵OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=$\frac{1}{3}$∠AOC=$\frac{1}{3}$×74°=($\frac{74}{3}$)°.
故答案是:($\frac{74}{3}$)°.
点评 本题考查了圆的认识:掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
15. 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )| A. | 2a-b | B. | b-2a | C. | -b | D. | b |
2.如果点P(a,2015)与点Q(2016,b)关于x轴对称,那么a+b的值等于( )
| A. | -4031 | B. | -1 | C. | 1 | D. | 4031 |
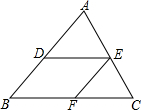 如图,DE∥BC,EF∥AB,则:
如图,DE∥BC,EF∥AB,则: