题目内容
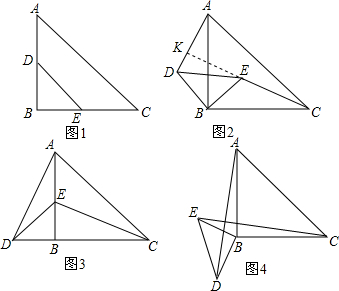
12.如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD、CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD
∴∠ABC-∠ABE=∠EBD-∠ABE即∠EBC=∠DBA
在△EBC和△DBA中
$\left\{\begin{array}{l}{BC=AB}\\{∠()=∠()}\\{BD=BE}\end{array}\right.$∠EBC=∠DBA
∴△EBC≌△DBA∴AD=EC,∠ECB=∠DAB∵∠ECB+∠ACE+∠CAB=90°
∴∠DAB+∠ACE+∠CAB=90°∴∠AKC=90°∴AD⊥EC
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD、CE.问(1)中线段AD、EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由.
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD、CE.请直接写出线段AD、EC间的数量关系和位置关系.
分析 (1)根据证明过程直接填空即可;
(2)先证△ADB与△CBE全等,得出CE=AD,和∠ECB=∠DAB,延长CE交AD于点F,由于∠DAB与∠ADB互余,从而∠ECB也与∠ADB互余,从而得征;
(3)方法与(2)相同;
解答 解:(1)∵∠ABC=∠EBD
∴∠ABC-∠ABE=∠EBD-∠ABE即∠EBC=∠DBA
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=AB}\\{∠(EBC)=∠(DBA)}\\{BD=BE}\end{array}\right.$
∴△EBC≌△DBA,
∴AD=EC,∠ECB=∠DAB,
∵∠ECB+∠ACE+∠CAB=90°
∴∠DAB+∠ACE+∠CAB=90°
∴∠AKC=90°,
∴AD⊥EC.
(2)成立.如图3,
延长CE交AD于F,
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBE=∠ABD}\\{BE=BD}\end{array}\right.$,
∴△EBC≌△DBA,
∴AD=EC,∠ECB=∠DAB,
∵∠DAB+∠ADB=90°,
∴∠ECB+∠ADB=90°,
∴AD⊥EC;
(3)如图4,设CE、AD交于点F,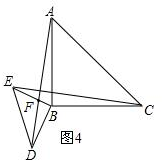
∵∠DBE=∠ABC=90°,
∴∠CBE=∠ABD,
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBE=∠ABD}\\{BE=BD}\end{array}\right.$
∴△EBC≌△DBA,
∴AD=EC,∠CEB=∠ADB,
∵∠ADB+∠DFB=90°,
∴∠CEB+∠AFE=90°,
∴AD⊥EC.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、三角形内角和性质、图形的旋转等知识点,难度不大,是一道基础题.事实上,本题得出了一个结论,即:两个全等的三角形如果有一个组对应相互垂直,那么另外两组对应边也相互垂直,这一结论在一些大型题目中可直接应用,会起到简化过程的作用.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | AB | B. | BC | C. | CA | D. | DE |
| A. | 外部 | B. | 内部 | C. | 圆上 | D. | 不能确定 |
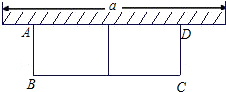 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).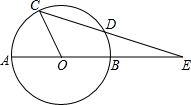 如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=74°,则∠E=($\frac{74}{3}$)°.
如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=74°,则∠E=($\frac{74}{3}$)°.