题目内容
11.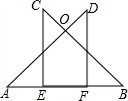 如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.
如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B,求证:OC=OD.
分析 先求出AF=BE,再利用“角边角”证明△ADF和△BCE全等,根据全等三角形对应边相等可得AD=BC,再根据等角对等边求出AO=BO,然后证明即可.
解答 证明:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
∵CE⊥AB,DF⊥AB,
∴∠AFD=∠BEC=90°
在△ADF和△BCE中,$\left\{\begin{array}{l}{∠A=∠B}\\{AF=BE}\\{∠AFD=∠BEC=90°}\end{array}\right.$,
∴△ADF≌△BCE(ASA),
∴AD=BC,
∵∠A=∠B,
∴AO=BO,
∴BC-BO=AD-AO,
即OC=OD.
点评 本题考查了全等三角形的判定与性质,等角对等边的性质,熟练掌握三角形全等的判断方法并准确确定出全等三角形是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1.某同学在计算某n边形的内角和时,不小心少输入一个内角,得到和为2005°.则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
19.下面计算正确的是( )
| A. | a2+a2=a4 | B. | (-a2)3=(-a)6 | C. | [(-a)2]3=a6 | D. | (a2)3÷a2=a3 |
16.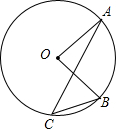 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )| A. | 30° | B. | 50° | C. | 60° | D. | 70° |
20.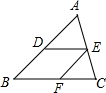 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
 如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.
如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.