题目内容
5.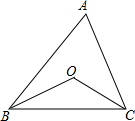 如图,已知点O是△ABC的两条角平分线的交点,
如图,已知点O是△ABC的两条角平分线的交点,(1)若∠A=30°,则∠BOC的大小是105°;
(2)若∠A=60°,则∠BOC的大小是120°;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
分析 (1)根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,根据三角形的内角和即可得到结论;
(2)根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,根据三角形的内角和即可得到结论;
(3)根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,根据三角形的内角和即可得到结论.
解答 解:(1)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=$\frac{1}{2}$∠A+90°=105°;
(2)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=$\frac{1}{2}$∠A+90°=120°;
(3)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=$\frac{1}{2}$∠A+90°=105°;
∴若∠A=n°,∠BOC=$\frac{1}{2}$n°+90°;
故答案为:105°,120°.
点评 本题考查了三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件以及三角形的外角通常情况下是转化为内角来解决.

| A. | 相等的两个角是对顶角 | |
| B. | 老师测量跳远成绩的依据是两点之间,线段最短 | |
| C. | 从直线外一点到这条直线上的各点所连接的线段中,垂线段最短 | |
| D. | 一个角一定不等于它的余角 |
| A. | 对角线相等四边形是矩形 | |
| B. | 对角线相互垂直平分四边形是菱形 | |
| C. | 对角线相互垂直且相等的平行四边形是正方形 | |
| D. | 对角线相互平分的四边形是平行四边形 |
| A. | 我县招聘考编老师,对应聘人员的面试 | |
| B. | 调查我市居民喜欢看热播电视剧《人民的名义》的收视情况 | |
| C. | 了解“天宫二号”飞行器零件的质量 | |
| D. | 旅客登上登上飞机前的安检 |
 如图,以CE为高的三角形有( )
如图,以CE为高的三角形有( )| A. | 9个 | B. | 10个 | C. | 11个 | D. | 12个 |
 如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.
如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.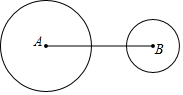 如图,⊙A、⊙B的半径分别为2、1,且AB=8,若作⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,与⊙B相交,则⊙C的半径在下列数字中可能是( )
如图,⊙A、⊙B的半径分别为2、1,且AB=8,若作⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,与⊙B相交,则⊙C的半径在下列数字中可能是( )